für einen Hochpunkt einer Funktion f(x) ist die notwendige Bedingung f'(x) = 0, die hinreichende Bedingung ist f''(x) < 0.
Tiefpunkt: Notwendige Bedingung f'(x) = 0, hinreichende Bedingung f''(x) > 0
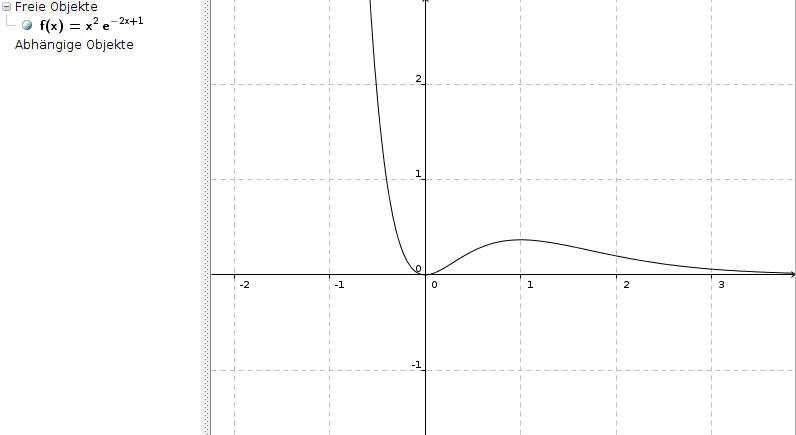
f(x) = x2 * e-2x+1
Zur Ableitung müssen wir zunächst einmal die Produktregel verwenden (uv)' = u'v + uv'
u = x2 | u' = 2x
v = e-2x+1
Zur Bestimmung der Ableitung von v müssen wir die Kettenregel anwenden: Innere Ableitung * äußere Ableitung
Innere Funktion: -2x + 1 | innere Ableitung: -2
Äußere Funktion: e-2x+1 | äußere Ableitung: e-2x+1
Insgesamt ist dann
f'(x) = 2x * e-2x+1 + x2 * (-2) * e-2x+1 = (-2x2 + 2x) * e-2x+1
Diese 1. Ableitung muss also sowohl für einen Hochpunkt als auch für einen Tiefpunkt = 0 sein.
e-2x+1 ≠ 0
-2x2 + 2x = 0 | :2
-x2 + x = 0
x * (-x + 1) = 0
x1 = 0
x2 = 1
Wir bilden die 2. Ableitung wie eben:
(uv)' = u'v + uv'
u' = (-2x2 + 2x)' = -4x + 2
v = e-2x+1
u = -2x2 + 2x
v' = -2 * e-2x+1
f''(x) = (-4x + 2) * e-2x+1 + (-2x2 + 2x) * (-2) * e-2x+1 = (-4x + 2 + 4x2 - 4x) * e-2x+1 = (4x2 - 8x + 2) * e-2x+1
Setzen wir x1 = 0 ein:
2 * e > 0, deshalb
Tiefpunkt (0|f(0))
Setzen wir x2 = 1 ein:
(4 - 8 + 2) * e-1 = -2 * 1/e < 0, deshalb
Hochpunkt (1|f(1))
Nun müsste man noch die y-Koordinaten der beiden Punkte berechnen, indem man einmal 0 und einmal 1 in die Ursprungsfunktion einsetzt, wozu ich aber jetzt keine Lust mehr habe :-)
Die Funktion sieht übrigens so aus:
Lieben Gruß