Aufgabe:
Für welche x>0 konvergiert die Reihe:
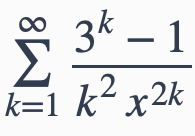
Text erkannt:
\( \sum \limits_{k=1}^{\infty} \frac{3^{k}-1}{k^{2} x^{2 k}} \)
Problem/Ansatz:
Tatsächlich stecke ich seit mehreren Stunden in einer Sackgasse hierbei.
Meine Überlegungen waren:
1. Es ist keine Potenzreihe (da es nicht in der allgemeinen Form vorliegt), weswegen ich mittels Konvergenzkriterien versuche, auf eine Lösung zu kommen.
2. Mit dem Quotientenkriterium und (weniger erfolgreich) mit dem Wurzelkriterium habe ich es also versucht. Hierbei habe ich den Betrag von a k+1 / ak <= 1 gesetzt, da ich ja möchte, dass die Reihe konvergiert.
Leider bekomme ich immer einen absolut undurchsichtigen Ausdruck heraus mit x und auch k. Ich weiß nicht, wie ich diese Ungleichung dementsprechend lösen soll.
Könnte mir jemand einen Tipp geben, wo mein Fehler ist und wie ich den Denkfehler beheben könnte?