Hallo,
Hier ein Lösungsansatz:
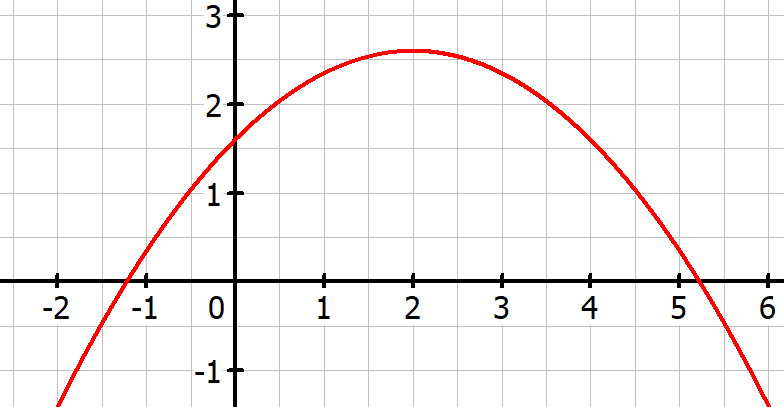
Gegeben:
- Scheitelpunkt S( 2|2,6)
- Punkt A(0| 1,6)
Gesucht: a) Parabelgleichung
b) Wo trifft der Wasserstrahl auf den Boden?
Scheitelpunktform
y = f(x) = a(x -xs)² + ys
y = a(x – 2)² + 2,6
P einsetzen in Funktion, um den Streckfaktor a zu bestimmen
1,6 = a( 0 – 2)² + 2,6
1,6 = 4a + 2,6
4a = - 1
a = - ¼
Scheitelpunktform in allgemeine Parabelform umwandeln
y = -1/4(x – 2)² + 2,6
y = -1/4( x² - 4x + 4) + 2,6
y = -1/4x² + x – 1 + 2,6
y = -1/4x² +x + 1,6
b) Nullstellen(y = 0) bestimmen
y = -1/4x² +x + 1,6 = 0
in pq-Form umwandeln
-1/4x² +x + 1,6 = 0 |: -(1/4)
x² - 4 x – 6,4 = 0
p = -4 q = -6,4
x1;2 = 2 ±√(4+6,4)
x1;2 = 2 ± 3,22
x1 = 5,22
Der Wasserstrahl trifft bei ≈ 5,22 m auf den Boden.
x2 = -1,22 entfällt