Warum wäre es dann bei dem folgenden Beispiel nur 5% und nicht 2.5% (--> 97.5%) ?
Aufgabe:
Eine Überprüfung von vergleichbaren, zufällig ausgewählten Betrieben verschiedener Branchen, bei der die Höhe X (in GE) der mit Ende 2006 unbezahlt gebliebenen Rechnungen erfasst wurde, brachte folgendes Ergebnis:

Text erkannt:
\begin{tabular}{|l|c|c|c|}
\hline Branche & Anzahl überprüfter Betriebe & Mittelwert \( \bar{x} \) & \( s_{n-1}^{2} \) \\
\hline Gastgewerbe & 45 & 36.76 & 123.87 \\
Bauwirtschaft & 30 & 61.22 & 137.22 \\
Metall & 45 & 64.95 & 163.53 \\
Uhren und Schmuck & 40 & 35.09 & 113.64 \\
Leder und Pelze & 45 & 71.32 & 214.31 \\
\hline
\end{tabular}
Geben Sie für die Branche Gastgewerbe ein 95-prozentiges Konfidenzintervall für den Er- wartungswert von X an.
Lösung:
Das 95%-Konfidenzintervall für den Erwartungswert μ lautet
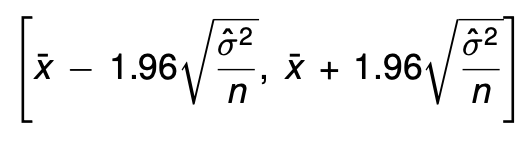
Text erkannt:
\( \left[\bar{x}-1.96 \sqrt{\frac{\hat{\sigma}^{2}}{n}}, \bar{x}+1.96 \sqrt{\frac{\hat{\sigma}^{2}}{n}}\right] \)
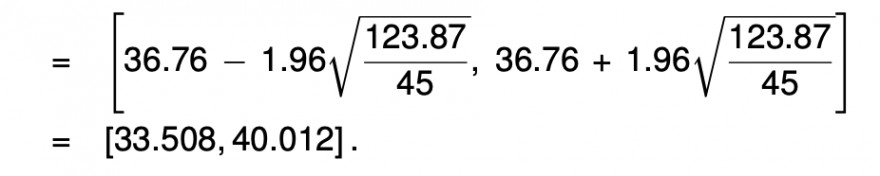
Text erkannt:
\( =\left[36.76-1.96 \sqrt{\frac{123.87}{45}}, 36.76+1.96 \sqrt{\frac{123.87}{45}}\right] \)
\( =[33.508,40.012] \)