Moin!
Ich versuche die Ableitung von 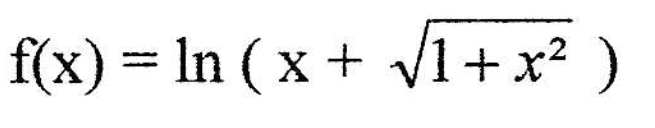
Text erkannt:
\( f(x)=\ln \left(x+\sqrt{1+x^{2}}\right) \)
zu lösen und habe dabei Probleme.
Das ist die Lösung laut Ableitungsrechner.net:
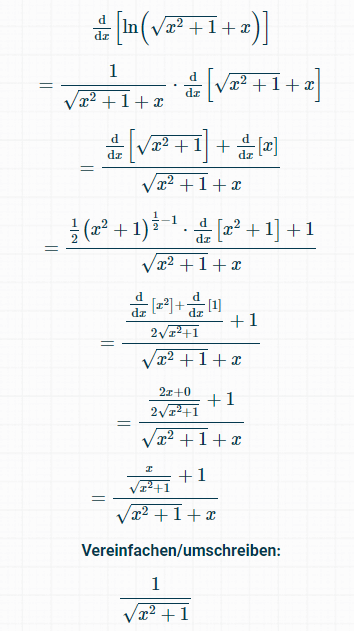
Text erkannt:
$$ \begin{array}{c} \frac{\mathrm{d}}{\mathrm{d} x}\left[\ln \left(\sqrt{x^{2}+1}+x\right)\right] \\ =\frac{1}{\sqrt{x^{2}+1}+x} \cdot \frac{\mathrm{d}}{\mathrm{d} x}\left[\sqrt{x^{2}+1}+x\right] \\ =\frac{\frac{\mathrm{d}}{\mathrm{d} x}\left[\sqrt{x^{2}+1}\right]+\frac{\mathrm{d}}{\mathrm{d} x}[x]}{\sqrt{x^{2}+1}+x} \\ =\frac{\frac{1}{2}\left(x^{2}+1\right)^{\frac{1}{2}-1} \cdot \frac{\mathrm{d}}{\mathrm{d} x}\left[x^{2}+1\right]+1}{\sqrt{x^{2}+1}+x} \\ =\frac{\frac{\mathrm{d}}{\mathrm{d} x}\left[x^{2}\right]+\frac{\mathrm{d}}{\mathrm{d} x}[1]}{2 \sqrt{x^{2}+1}}+1 \\ \sqrt{x^{2}+1}+x \\ =\frac{\frac{2 x+0}{2 \sqrt{x^{2}+1}}+1}{\sqrt{x^{2}+1}+x} \\ \frac{x}{\sqrt{x^{2}+1}}+1 \\ \sqrt{x^{2}+1}+x \end{array} $$
Vereinfachen/umschreiben:
\( \frac{1}{\sqrt{x^{2}+1}} \)
Text erkannt:
\( f(x)=\ln \left(x+\sqrt{1+x^{2}}\right)
An der Lösung verstehe ich 2 Dinge nicht:
1. Muss man in der 2. Zeile die Ableitung wirklich nur mit dem Zähler des linken Bruches multiplizieren? (und ist das immer der Fall?)
2. Wie vereinfacht man die vorletzte Zeile in die letzte Zeile?