Hier ein Bild der Szene (drauf klicken)
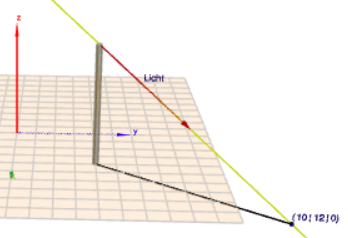
Die Geradengleichung für den Lichtstrahl, der 'durch' die Spitze des Stabes scheint, ist:$$g: \quad \vec x = A + \vec v \cdot t = \begin{pmatrix}4\\ 4\\ 6\end{pmatrix} + \begin{pmatrix}3\\ 4\\ -3\end{pmatrix} t$$für \(t=2\) kommt man zum Schattenpunkt. Und die Länge (10) des Schattens kann man via Pythagoras berechnen.
