Hallo,
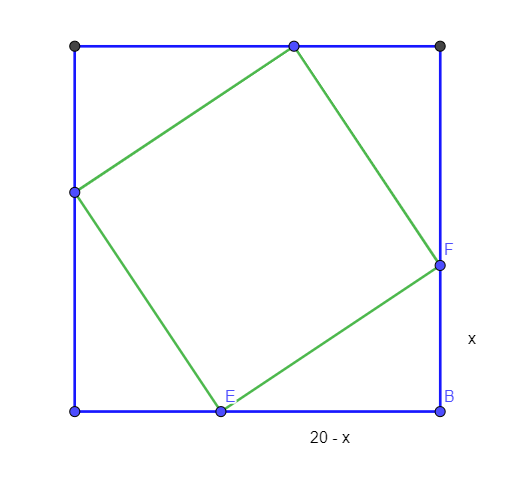
Die Seitenlänge a des kleinen, grünen Quadrates ist die Hypotenuse des Dreiecks EBF
\(a=\sqrt{(20-x)^2+x^2}\)
Der Flächeninhalt des grünen Quadrates ist
\(A=a^2=(20-x)^2+x^2\)
Multipliziere die Klammer aus und fasse zusammen, dann erhältst du
\(A=400-40x+x^2+x^2\\=2x^2-40x+400\)
Bilde die 1. Ableitung, setze sie gleich 0 und löse nach x auf:
\(A'=4x-40\\4x-40=0\\ x= 10\)
Gruß, Silvia