Aufgabe:
Eine dreieckige Waldfläche soll entsprechend obigem Schaubild in Ackerflächen umgewandelt werden, wobei die braun gefärbte Fläche künftige Kartoffelacker sein sollen, die an sechs Landwirte verteilt werden sollen. Die Ackerflächen sollen möglichst groß sein, sodass die Landwirte ein möglichst flächengroßes Teil erhalten werden.
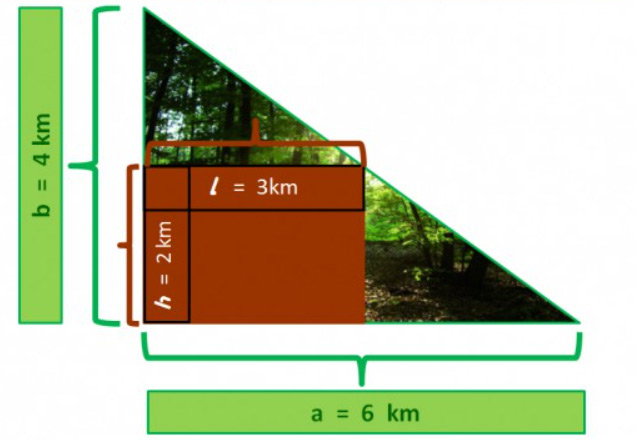
Wie groß könnte die braun gefärbte Fläche bei den angegebenen Maßen maximal werden, wenn die Fläche eine rechteckige Form haben soll?
Ich habe mir bereits grafisch Überlegungen dazu gemacht.
Das dreieckige Waldstück ist 6 km lang und 4 km breit.
Wie groß kann nun die rechteckige Ackerfläche maximal sein?
Habe folgende Aufgaben dazu:
1. Bestimme die Zielfunktion mit den 2 Variablen l und h.
2. Welche Definitionsmenge für die Länge l ist für die rechteckige Ackerfläche sinnvoll?
→ D = ]0 ; 6[ → Die Werte 0 und 6 würde ich ausschließen.
Kann eine Seite der Ackerfläche auch weniger als 1 km breit sein?
3. Bringe die Seiten l und h der rechteckigen Ackerfläche in einen Zusammenhang und stelle dabei die Nebenbedingungen auf.
h = 4 - 6/4 · l Stimmt das?
4. Stelle die Flächenfunktion der Ackerfläche unter Gebrauch der Nebenbedingung aus Aufgabe 3 in Abhängigkeit der Seite l der Ackerfläche dar und bestimme dabei die Zielfunktion, die nur noch eine Variable enthält.
5. Berechne die Länge l der rechteckigen Ackerfläche so, dass der größtmögliche Flächeninhalt erzeugt wird.
Bestimme dazu die relativen bzw. absoluten Extremstellen.
→ Erste Ableitung der zusammengesetzten Funktion
6. Könnte der Flächenplaner auch eine größere Fläche erhalten, wenn er die Fläche anders in das dreieckige Waldstück hineinlegt?
→ Nein, denn die Fläche ist bereits maximal bestimmt worden. Stimmt das?
Bitte um Ergänzungen und Vervollständigung des Rechenwegs.