Aufgabe:
Nicht-Norm eines Funktionenraumes
Problem/Ansatz:
Hallo :)
Kann mir jemand hierbei helfen ?

Text erkannt:
Nicht-Norm eines Funktionenraumes
Sei \( X \) der Raum der integrierbaren Funktionen \( f:[a, b] \rightarrow \mathbb{R} \). Zeigen Sie, dass \( \|f\|_{L^{1}} \) keine Norm auf \( X \) ist.
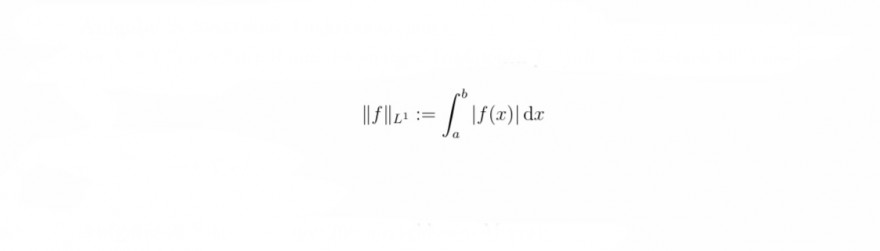
Text erkannt:
\( \|f\|_{L^{1}}:=\int \limits_{a}^{b}|f(x)| \mathrm{d} x \)