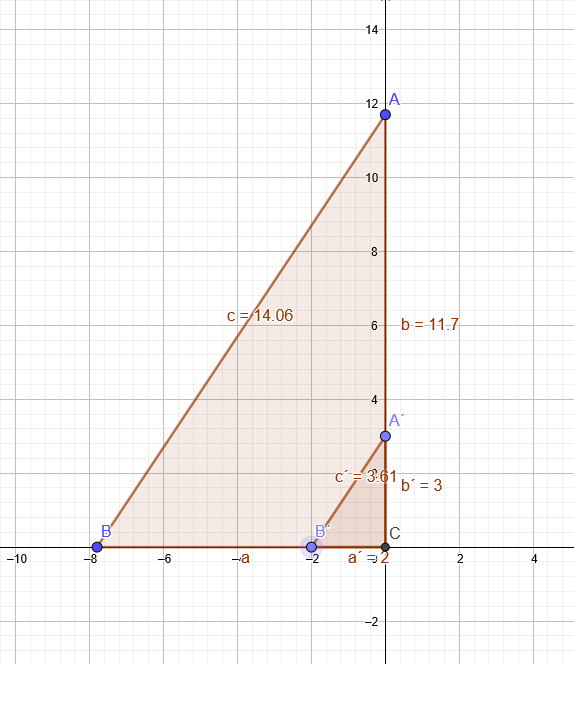
In einem rechtwinkligen Dreieck misst die längste Seite 14cm. Das Verhältnis der Seitenlängen a und c beträgt 2:3
b´=\( \sqrt{a´^2+c´^2} \) b´=\( \sqrt{4+9} \)≈3,61
\( \frac{2}{3,61} \)=\( \frac{2+x}{14} \)
7,22+3,61x=28
x≈5,8
a=2+5,8=7,8
\( \frac{2}{7,8} \)=\( \frac{3}{c} \)
c≈11,7