Hallo,
schreibe die Quadrik in der Matrix-Vektor-Form:$$(x\, y \, z)\begin{pmatrix}0 & 0.5 & 0.5\\ 0.5 & 0 & 0.5\\ 0.5 & 0.5 & 0 \end{pmatrix}\begin{pmatrix} x\\y\\z \end{pmatrix}-1=0$$ Wenn es dir nur um den Typ geht, kannst du die erweiterte Darstellungsmatrix anschauen \(\overline{A}=\begin{pmatrix} A & b \\ b^T & c\end{pmatrix}\), wobei von der typischen Form \(x^TAx+b^Tx+c=0\) ausgegangen wird.
Es gilt dann:
- Kegeliger Typ: \( \operatorname{rang}(\bar{A})=\operatorname{rang}(A \mid b)=\operatorname{rang}(A) \)
- Mittelpunktsquadrik. \( \operatorname{rang}(\bar{A})>\operatorname{rang}(A \mid b)=\operatorname{rang}(A) \)
- Parabolischer Typ: rang \( (A \mid b)>\operatorname{rang}(A) \)
Eine Quadrik heißt dabei ausgeartet, falls \( \operatorname{det} \bar{A}=0 \)
Quelle: https://de.wikipedia.org/wiki/Quadrik#Typen
Um genauer zu bestimmen, um was es sich handelt, ist es ggf. hilfreich eine Hauptachsentransformation durchführen.
Hier muss nur in Hauptachsenlage gedreht werden. Es gilt, weil \(b^T=0\) ist keine Translation.
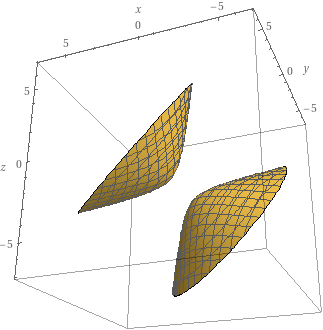
Musterlösung: Zweischaliges Hyperboloid