Aufgabe:
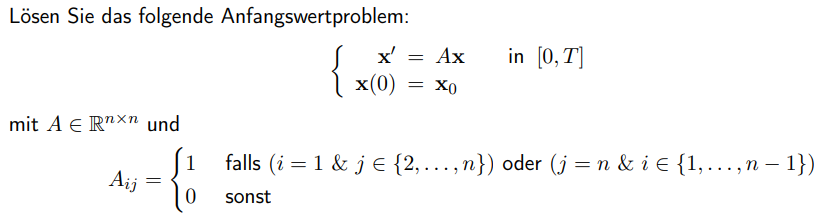
Text erkannt:
Lösen Sie das folgende Anfangswertproblem:
$$ \left\{\begin{aligned} \mathbf{x}^{\prime} &=A \mathbf{x} \quad \text { in }[0, T] \\ \mathbf{x}(0) &=\mathbf{x}_{0} \end{aligned}\right. $$
mit \( A \in \mathbb{R}^{n \times n} \) und
$$ A_{i j}=\left\{\begin{array}{ll} 1 & \text { falls }(i=1 \& j \in\{2, \ldots, n\}) \text { oder }(j=n \& i \in\{1, \ldots, n-1\}) \\ 0 & \text { sonst } \end{array}\right. $$
Problem/Ansatz:
ich komme bei diesem Anfangswertproblem nicht weiter.
Meine Überlegungen dazu waren, dass 0 der Eigenwert mit Vielfachheit n ist, da auf der Diagonalen ja nur 0er stehen. Und das sind ja bei einer Dreiecksmatrix die Eigenwerte.
Jedoch bekomme ich keine Eigenvektoren bestimmt und weiß nicht, wie die Lösungsmatrix aussehen soll.
Vielen Dank für die Hilfe.