Hallo,
1. Teil
Du bestimmst die Nullstellen in Abhängigkeit von p, bildest du Stammfunktion und setzt die Nullstellen als Integralgrenzen ein.
Wenn du die Lösung des 2. Teil kennst, wirst du das ja schon gemacht haben, oder nicht?
Gruß, Silvia
Teil 3
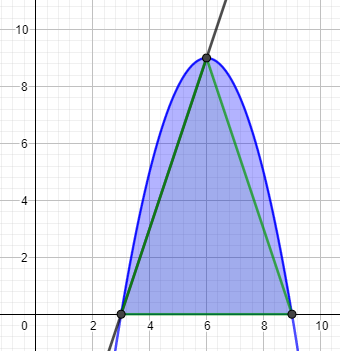
Die Nullstellen und der Scheitelpunkt der Parabel bilden ein Dreieck. Berechne den Flächeninhalt dieses Dreiecks und ziehe ihn von dem Flächeninhalt des Integrals ab. Teile das Ergebnis durch 2 und berechne den Anteil an der blauen Fläche.
Du kannst natürlich auch die Gleichung der Geraden durch Nullstelle und Scheitelpunkt bestimmen und den Flächeninhalt zwischen Parabel und Gerade bestimmen. Ich finde das jedoch aufwendiger.
Melde dich, falls du dazu noch Fragen hast.