\( H=\left\{(x, y) \mid \frac{x}{a^{2}}-\frac{y}{b^{2}}=1\right\} \)
Hallo,
da fehlen Quadrate:
\( H=\left\{(x, y) \mid \frac{x^2}{a^{2}}-\frac{y^2}{b^{2}}=1\right\} \)
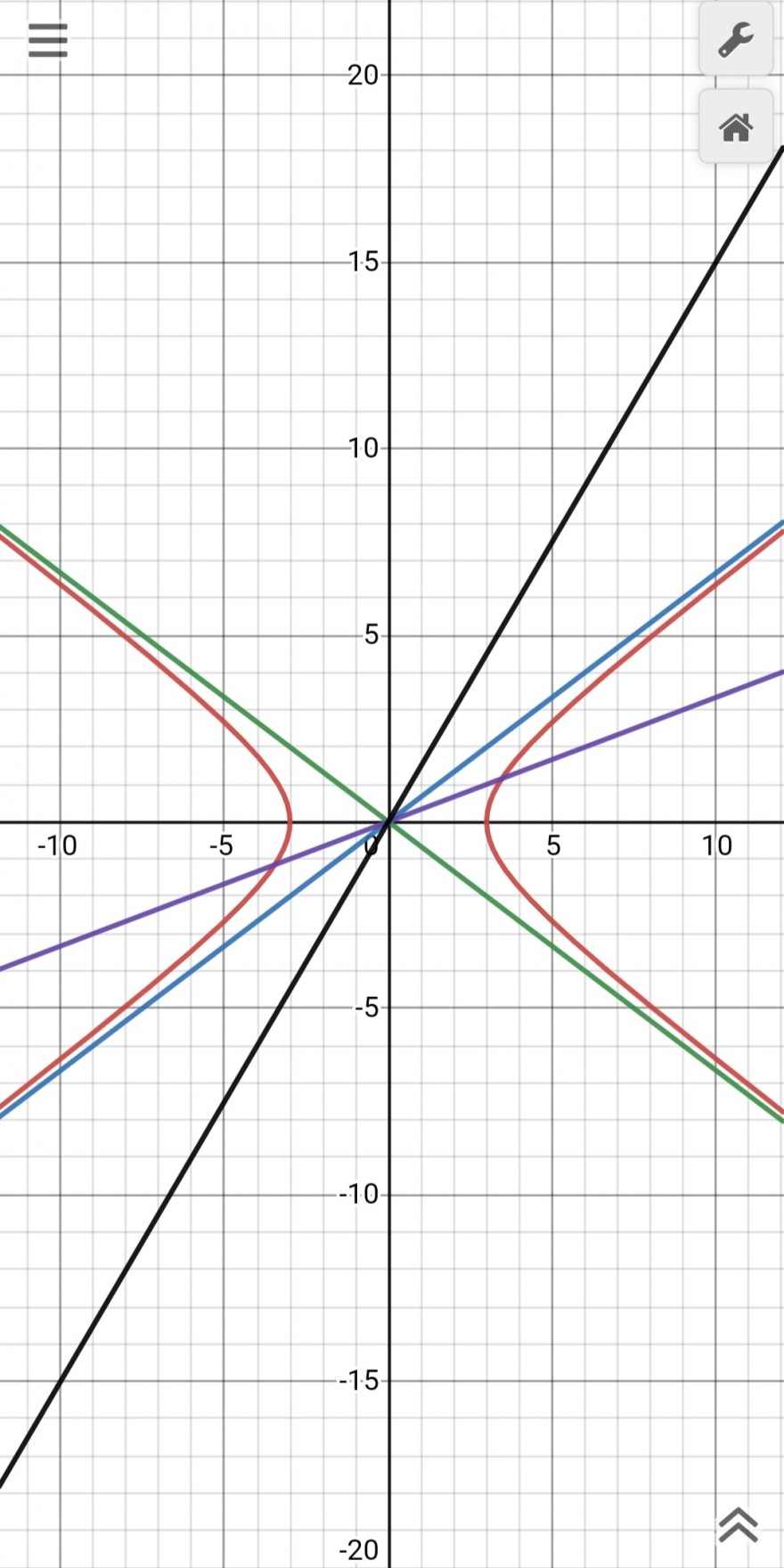
Die Asymptoten (grün, blau) haben die Gleichungen
\(y=\pm\frac b a \cdot x\).
Sie schneiden die Hyperbel nicht (schwarz).
Alle Ursprungsgeraden, für deren Steigung m gilt |m|<|b/a|, schneiden die Hyperbel. Alle anderen schneiden sie jeweils in zwei Punkten (violett).