habe aber noch ein par Unklarheiten: warum ist die obere Grenze des x integrals 2pi?
Bei mir gibt es weder ein Integral über \(x\) noch eine oberer Grenze von \(2\pi\). Und wenn Dein Lösungsansatz ein Doppelintegral ist, dann lautet das womöglich$$V =\int\limits_{r=1}^2 \,\int\limits_{\varphi = 0}^{2\pi} rf(r)\,\text d\varphi\,\text dr$$
Etwa weil es sich um einen Kreis handelt der 360 ° hat?
Ja sicher. Das innere Integral ist dann schlicht$$\int\limits_{\varphi = 0}^{2\pi} rf(r)\,\text d\varphi = \left.rf(r) \varphi\right|_{\varphi = 0}^{2\pi} = 2\pi rf(r)$$da der Ausdruck \(rf(r)\) in keiner Weise von \(\varphi\) abhängt, ist das trivial.
Zum Verständnis: ein Integral ist immer eine Summe. Und bei einer Summe ist es egal in welcher Reihenfolge man die Summanden addiert. Natürlich kann man sich bei der Wahl der Reihenfolge einmal mehr und einmal weniger Arbeit machen ;-)
Ein Volumenintegral \(\int\,\text dV\) ist ist immer ein Dreifachintegral - also über die drei Dimensionen des Raums. Wenn in Deinem Fall ein Doppelintegral vorliegt, dann ist es wahrscheinlich$$V = \int_G f(r) \,\text dG$$D.h. Das Integral \(\int \,\text dz\) von \(z=0\) bis \(z=f(r)\) ist bereits gelöst, da ebenfalls trivial. Das \(G\) steht für das (2-dimensionale) Gebiet in der xy-Ebene, welches durch die beiden Kreisringe begrenzt wird.
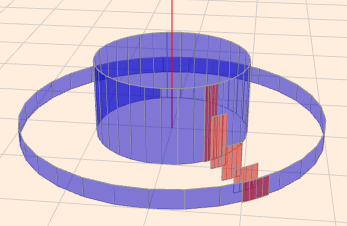
oben im Bild habe ich versucht, das darzustellen. Die blauen Ringe begrenzen den Körper in Richtung \(r\) - also radial. Jede von diesen kleinen roten Säulen hat die Höhe \(f(r)\), die Breite \(r \,\text d\varphi\) und die Dicke \(\text dr\). D.h. die Fläche \(\text dG\) die so eine Säule in der xy-Ebene belegt ist $$\text dG = r \,\text d\varphi\,\text dr$$Setzte das in \(\int_G\) ein und Du erhältst$$V = \int_G f(r) r \,\text d\varphi\,\text dr$$Und um das Gebiet \(G\) zu erfassen, integrierst Du einmal über den Kreis \(\varphi =0\) bis \(2\pi\) und einmal über den Radius \(r=1\) bis \(2\)$$V =\int\limits_{r=1}^2 \,\int\limits_{\varphi = 0}^{2\pi} rf(r)\,\text d\varphi\,\text dr$$Frage ruhig nochmal nach, wenn noch was unklar geblieben ist.