Moin!
7) Tauchkugel
a)
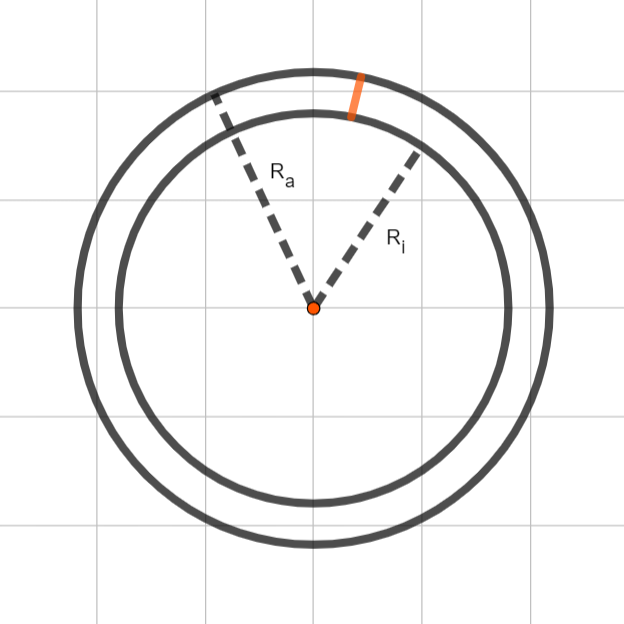
Aus dem Text können wir herauslesen, dass die Tauchkugel einen Durchmesser von \(2,18\) m hat. Nicht verwechseln mit Radius! Der Radius ist hier \(R_a = \frac{2,18}{2} = 1,09\) m. Die Wandstärke beträgt \(12\) cm (orange in der Skizze), womit sich ein innerer Radius von \(R_i = 1,09 - 0,12 = 0,97\) m ergibt. Weiterhin wissen wir, dass der Stahl pro \(1\) cm\(^3\) \(7,8\) g wiegt. Nun haben wir alles, um die Aufgabe bearbeiten zu können. Das Volumen einer Vollkugel beträgt
\(V_{\text{voll}} = \frac{4}{3}\pi R_a^3\).
Da wir aber keine Vollkugel, sondern Hohlkugel haben, müssen wir
\(V_{\text{Tauchkugel}} = V_{R_a} - V_{R_i}\)
berechnen, um das Volumen der Tauchkugel zu erhalten. Jetzt müssen wir uns an einer Formel aus der Physik erinnern: Masse ist gleich Dichte mal Volumen,
\(m = \rho \cdot V\).
Wichtig: Am Ende die Masse, wenn noch nicht getan, in Tonnen umrechnen!
b)
Ich gehe davon aus, dass wir die gleiche Masse betrachten sollen, die wir in der a) berechnet haben. Nutze also geschickt eine bereits genannte Formel und stell diese nach dem Radius \(r_{\text{Vollkugel}}\) um. Bedenke dabei, dass wir diesmal eine Vollkugel betrachten.
8) Dach bedecken
a)
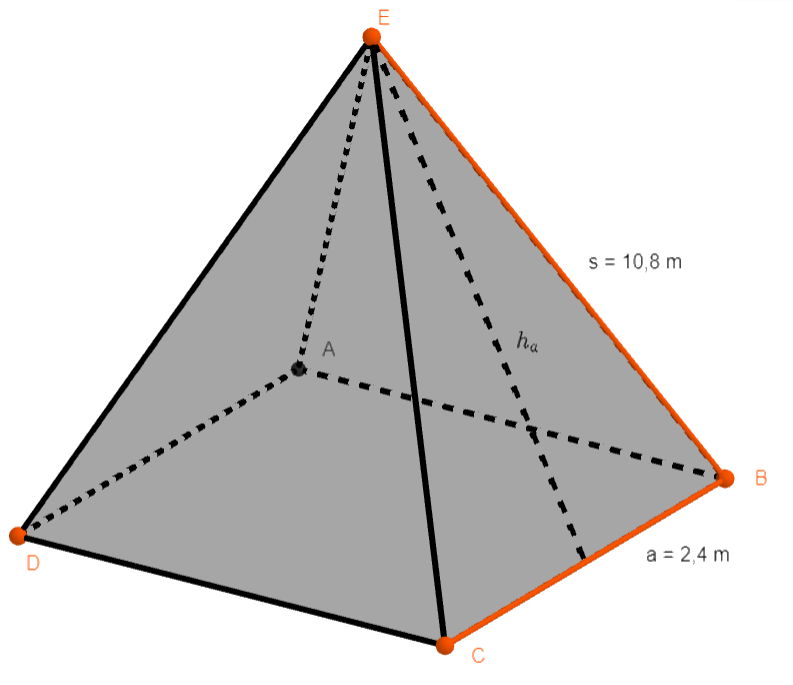
In der obigen Skizze unseres Daches sind alle Informationen, die wir haben, eingezeichnet. Wir wollen nun berechnen, wieviel Quadratmeter Kupferblech wir für eine neue Dachbedeckung brauchen. Den Boden von einem Dach brauchen wir nicht neu bedecken, sondern nur die, um es geometrisch auszudrücken, Mantelfläche. Die Mantelfläche einer quadratischen Pyramide beträgt
\(M_{\text{Dach}} = 2a \cdot h_a\).
Was uns also noch fehlt ist \(h_a\). Das bekommen wir aber ganz schnell heraus, indem wir an den Herrn Pythagoras denken.
b)
Nachdem wir nun wissen, wie viel Blech wir für ein neues Dach benötigen, wollen wir wissen, was uns der Spaß kosten wird. Wir suchen Kuperblech aus, was pro 1 m\(^2\) \(65\) Euro kostet. Dabei soll mit 4% Verschnitt gerechnet werden. Stelle also die Formel für die Kosten ohne Verschnitt und einmal nur den Verschnitt auf. Diese beiden Formeln lassen sich dann zu einer Formel vereinigen. Diese hat in etwa in Form
\(\text{Kosten} = \alpha \cdot \beta (1 + \gamma)\),
wobei \(\alpha,\ \beta\) und \(\gamma\) von dir bestimmt werden sollen.
Lg