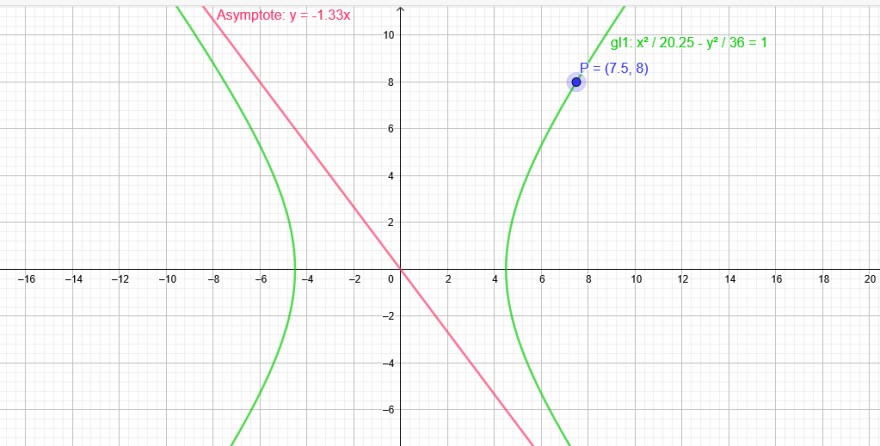
\(y=\pm\frac{b}{a}x\)
4x + 3y =0 → y=-\( \frac{4}{3} \)*x
1.)\( \frac{b^2}{a^2} \)=\( \frac{16}{9} \) → b^2=\( \frac{16}{9} \)a^2 in 2.) einsetzen
\( \frac{x^2}{a^2} \)-\( \frac{y^2}{b^2} \)=1
P(7,5|8)
2.)\( \frac{7,5^2}{a^2} \)-\( \frac{8^2}{b^2} \)=1
\( \frac{7,5^2}{a^2} \)-\( \frac{8^2}{b^2} \)=1
a^2=20,25
b^2=36
\( \frac{x^2}{20,25} \)-\( \frac{y^2}{36} \)=1