Hi Erik,
Die Gerade g enthält die Punkte (-3|-5) und Q(2|3)
Geradengleichung allgemein
y = mx + b
Zuerst bestimmen wir m, indem wir die "y-Differenz" durch die "x-Differenz" dividieren:
[3 - (-5)]/[2 - (-3)] = 8/5
Also
y = 8/5 * x + b
Wir setzen einen Punkt, zum Beispiel Q, in diese Gleichung ein, um b zu erhalten:
3 = 8/5 * 2 + b
b = 3 - 16/5 = -1/5
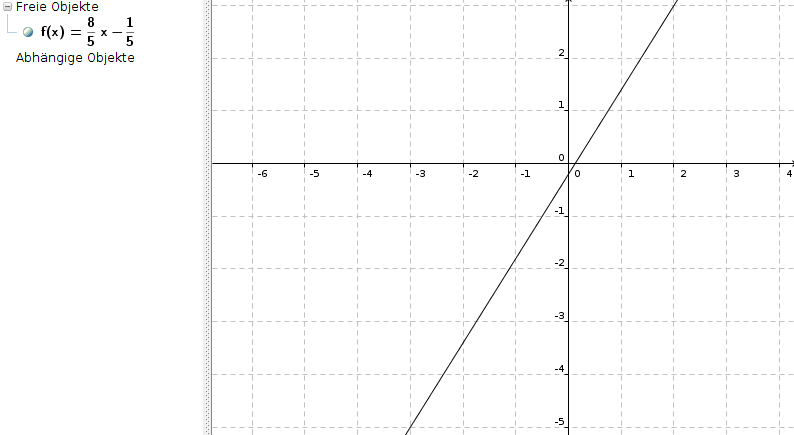
Die Geradengleichung lautet damit
y = 8/5 * x - 1/5
Liegt der Punkt (6|8) auf der geraden g?
Wir setzen einfach die Koordinaten in die Geradengleichung ein:
8 = 8/5 * 6 - 1/5 = 47/5
Das ist unwahr, also liegt (6|8) nicht auf der Geraden!
Besten Gruß