Bestimmen Sie angenähert durch Anlegen einer Näherungstabelle die Steigung von f an der Stelle x0

Question

Aufgabe:

Steigung (tabellarisch)

Bestimmen Sie angenähert durch Anlegen einer Näherungstabelle die Steigung von f an der Stelle x0

a) f(x) = x², x0 = 1

b) f(x) = ¼x³, x0 = 2

Ich danke Ihnen im Voraus für die Hilfe.
Problem/Ansatz:

Wie muss ich das genau berechnen?

Answer 1

Hallo,

wähle einen weiteren Punkt auf dem Graphen und bilde die Steigung der Sekante zwischen den beiden Punkten mithilfe des Differenzquotieten: \(m=\frac{f(x_1)-f(x_0)}{x_1-x_0}\)

Für Aufgabe a) wähle ich \(x_1=2\)

Dann ergibt sich für die Sekantensteigung \(m=\frac{4-1}{2-1}=3\)

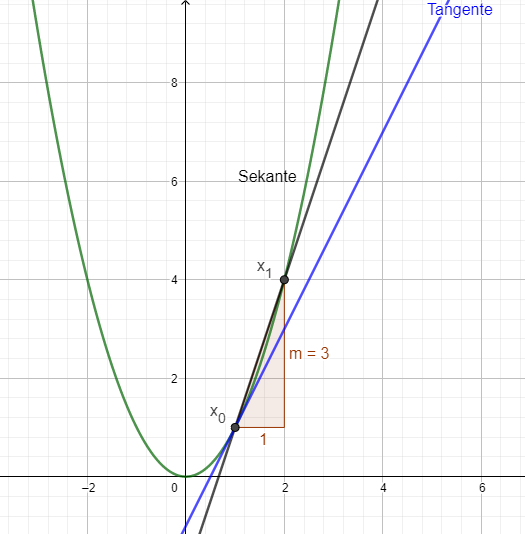
Um dich der Steigung der Tangente an der Stelle \(x_0=1\) anzunähern, verringerst du die Abstände. Das könnte dann so aussehen.

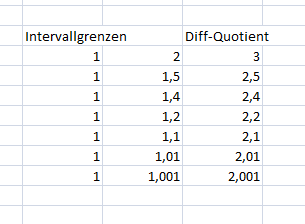
Für b) gehst du genauso vor.

Gruß, Silvia

Answer 2

a) mathematisch:

((1+h)^2-1^2)/ h = (1+2h+h^2-1)/h = (2h+h^2)/h = 2+h

lim (2+h) = 2 für h gegen 0

-> f '(1)= 2

b) (1/4(2+h)^3 - 1/4*2^3)/h = ...