Hallo liko,
überrasche doch Deinen Lehrer mal mit einer ungewöhnlichen Lösung und löse es zeichnerisch. Zeichne dazu die Punkte \(N(2|\,0)\) und \(M(1/2|\,-\!9/4)\) in ein Koordinatensystem ein, so wie hier.
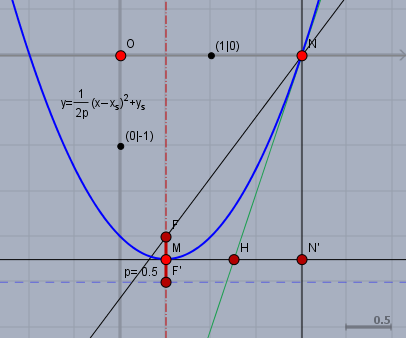
Die Senkrechte durch \(M\) (rot Strich-Punkt) ist die Symmetrieachse \(a\) der Parabel, da \(M\) der Scheitel ist. Die Senkrechte durch \(N\) schneidet die Waagerechte durch \(M\) (beide schwarz) in \(N'\). Der Punkt \(H\) halbiert die Strecke \(MN'\) und die Gerade durch \(HN\) (grün) ist die Tangente \(t\) an die gesuchte Parabel in \(N\).
Spiegele nun die Senkrechte durch \(N\) an der Tangenten \(t\). Das Spiegelbild schneidet die Symmetrieachse \(a\) im Brennpunkt \(F(1/2|\, -\!2)\). Spiegele den Punkt \(F\) an \(M\) - man erhält \(F'(1/2|\,-\!5/2)\). Die Strecke \(|FF'|\) ist der Halbparameter \(p\) der Parabel. \(p\) ist hier \(p=1/2\), wie aus der Zeichnung zu entnehmen ist.
Wenn man nun noch weiß, dass eine Parabel mit \(p\) und Scheitelpunkt \((x_s|\,y_s)\) wie folgt dargestellt werden kann:$$y=\frac1{2p}(x-x_s)^2+y_s$$brauchst Du nur noch einsetzen:
[spoiler]
$$y = \frac 1{2 \cdot \frac 12} \left(x-\frac12\right)^2 - \frac 94\\\phantom{y=} = \left(x-\frac12\right)^2 - \frac 94\\\phantom{y=} = x^2-x -2$$
[/spoiler]
Gruß Werner