Begründen Sie, dass für die Steigung mf und mg orthogonaler Geraden allgemein gilt: mf x mg = -1

Question

Aufgabe:

Begründen Sie, dass für die Steigung mf und mg orthogonaler Geraden allgemein gilt: mf x mg = -1

Answer 1

Aloha :)

Die Steigung \(m_f\) der Geraden \(f\) gibt Auskunft über den Steigungswinkel \(\alpha_f\) der Geraden. Gleiches gilt für die Steigung \(m_g\) der Geraden \(g\). Konkret gilt:$$m_f=\tan(\alpha_f)\quad;\quad m_g=\tan(\alpha_g)$$Wenn die Geraden nun senkrecht aufeinander stehen, gilt \(\alpha_f=\alpha_g\pm\frac{\pi}2\). Wir bestimmen das Produkt der beiden Steigungen:$$m_f\cdot m_g=\tan\left(\alpha_g\pm\frac\pi2\right)\cdot\tan\left(\alpha_g\right)=\frac{\sin\left(\alpha_g\pm\frac\pi2\right)}{\cos\left(\alpha_g\pm\frac\pi2\right)}\cdot\frac{\sin\left(\alpha_g\right)}{\cos\left(\alpha_g\right)}$$$$\phantom{m_f\cdot m_g}=\frac{\pm\cos\left(\alpha_g\right)}{\mp\sin\left(\alpha_g\right)}\cdot\frac{\sin\left(\alpha_g\right)}{\cos\left(\alpha_g\right)}=\frac{(\pm1)\cdot\cancel{\cos\left(\alpha_g\right)}}{(\mp1)\cdot\cancel{\sin\left(\alpha_g\right)}}\cdot\frac{\cancel{\sin\left(\alpha_g\right)}}{\cancel{\cos\left(\alpha_g\right)}}=-1$$

Answer 2

Ich erkläre das meist anhand einer sehr einfachen Skizze

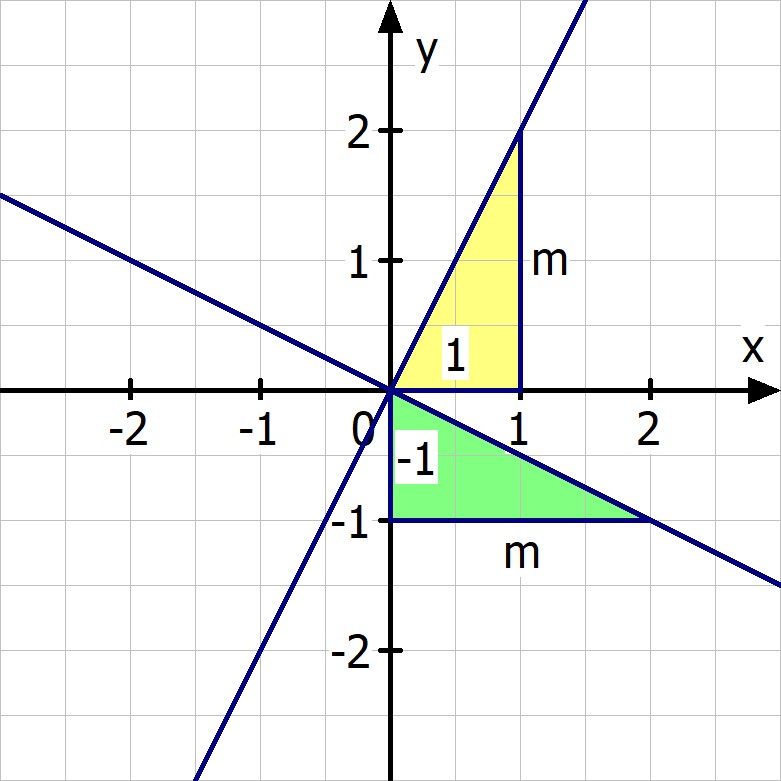
Schauen wir uns das gelbe Steigungsdreieck an, dann ist die Steigung dort sicher m.

Dreht man dieses Dreieck jetzt um 90 Grad und betrachtet damit das grüne Steigungsdreieck, so ist die Steigung dort -1/m

Bildet man jetzt das Produkt

m * (-1/m) = -1

So ist offensichtlich, dass das Produkt zueinander senkrechter Steigungen immer -1 sein muss.