Hallo,
\(y=(x-2)^2-1,4\)
y ist nichts anderes als der Funktionswert.
Setze also für y 2,6 ein und löse nach x auf:
\(2,6=(x-2)^2-1,4\)
[spoiler]
\(2,6=x^2-4x+4-1,4\\2,6=x^2-4x+2,6\quad |-2,6\\ 0=x^2-4x\quad \text{x ausklammern}\\0=x\cdot (x-4)\\\text{Satz vom Nullprodukt anwenden: Ein Produkt ist null, wenn einer der Faktoren null ist}\\ x=0\quad x-4=0\Longrightarrow x=4\)
Graphisch sieht das so aus:
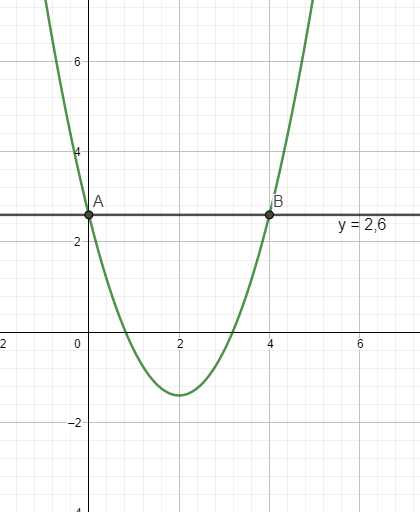
[/spoiler]
Gruß, Silvia