Hallo,
Doch wenn ihr euch jetzt 30° nach links rotiert, wie schnell kann man maximal werden?
Die Wahrheit ist: beliebig schnell! (jeglicher Widerstand vernachlässigt)
Die Windgeschwindigkeit beträgt 45 km/h, also fahrt ihr auch mit 45 km/h, da es schneller natürlich nicht geht
Das gilt für einen Ballon, der mit dem Wind getrieben wird (fährt), aber nicht für ein Segelboot.
Die Verhältnisse am Segelboot sehen so aus:
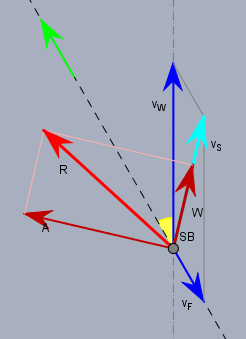
Oben sind alle Windgeschwindigkeiten blau und alle Kräfte rot eingezeichnet. Der Wind weht in der Skizze senkrecht nach oben. Die Richtung der Bewegung des Segelboots (SB) ist durch den grünen Pfeil dargestellt. Der gelbe Winkel ist der besagte 30°-Winkel aus der Aufgabe.
Das (bzw. die) Segel eines (klassischen) Segelboots wirken wie Tragflächen. D.h. sie erzeugen eine Auftriebskraft \(A\), die senkrecht(!) zu der Geschwindigkeit \(v_S\) steht, mit der die umgebende Luft auf das Segel trifft. Dieser 'Wind' ist der sogenannte scheinbare Wind, der sich aus dem wahren Wind \(v_W\) (hier der senkrechte Pfeil) und dem Fahrtwind \(v_F\) zusammen setzt. Den scheinbaren Wind \(v_S\) habe ich als hellblauen Pfeil dargestellt.
Dieser Wind \(v_S\) erzeugt am Segel die Auftriebskraft \(A\) und einen Widerstand \(W\). Die Resultierende \(R\) treibt das Boot nach vorn. Das Boot kann genau dann in die gezeigte Richtung fahren, wenn eine Komponente von \(R\) in Fahrtrichtung zeigt und diese Komponente größer ist als der Widerstand des Bootes im Wasser.
Vernachlässigt man nun weitgehend jeden Widerstand, so sieht das so aus:
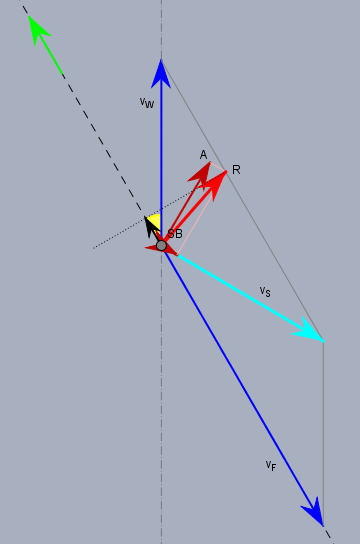
Die Geschwindigkeit des Bootes entspricht dem blauen Pfel \(v_F\) (natürlich in der Gegenrichtung). Man kann \(v_F\) beliebig vergrößern, wenn der Widerstand \(W\) zu 0 wird, bleibt immer eine Komponente (schwarzer Pfeil) von \(R\) übrig, der das Boot nach vorn treibt.
cosα = a / c <=> cos30 = 45/ c <=> 45/cos30 = 51,96 km/h
diese Rechnung ist physikalischer Unsinn! Du nimmst hier an, dass sich das Segelboot genauso schnell in Windrichtung bewegt, wie der Wind selbst. Das sähe dann so aus:
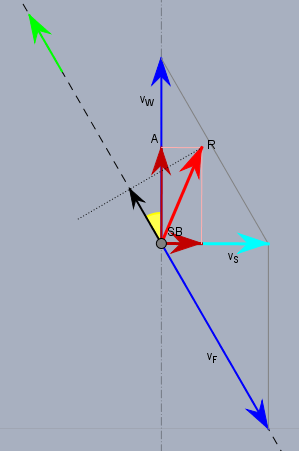
D.h. der scheinbarer Wind \(v_S\) steht in diesem Fall genau senkrecht auf der Windrichtung, die durch den wahren Wind \(v_W\) vorgegeben ist. Aber warum sollte sich das Segelboot jetzt nicht schneller oder langsamer (bei höherem WIderstand) bewegen dürfen? Aus Sicht des Bootes ist das kein besonderer Fall. Wenn Du hier am Steuer des Bootes stehst, so würdest Du nur feststellen, dass der Wind mit einem Winkel von 60° schräg von links vorne kommt.
Frage ruhig nach, wenn was unklar ist. Stammt die Frage so aus einem Schulbuch?
Gruß Werner