a) f(x)= \( \frac{x}{x^2-1} \)
Nullstellen: Zähler =0
x=0
Polstellen: Nenner =0
x^2-1=0
x^2=1|\( \sqrt{} \)
x₁=1
x₂=-1
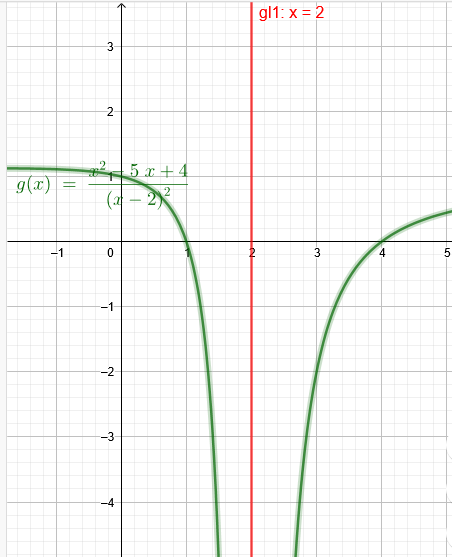
b) \( g(x)=\frac{x^{2}-5 x+4}{(x-2)^{2}} \)
Nullstellen:
\( x^{2} \) - 5x+4=0
\( x^{2} \) - 5x=-4
(x-\( \frac{5}{2} \))^2=-4+(\( \frac{5}{2} \))^2=\( \frac{9}{4} \)|\( \sqrt{} \)
1.)x-\( \frac{5}{2} \)=\( \frac{3}{2} \)
x₁=4
2.)x-\( \frac{5}{2} \)=-\( \frac{3}{2} \)
x₂=1
Polstelle:
(x-2)^2=0
x=2