Berechne den Inhalt A der von den Graphen der Funktionen f und g eingeschlossenen Fläche.

Question

Aufgabe:

Die Graphen von f und g besitzen zwei Schnittpunkte. Berechnen sie den Inhalt A der von den Graphen der Funktion f und g eingeschlossenen Fläche.

Problem/Ansatz:

f(x)=0,5x^2-2

g(x)=-0,5x+1

Ich weiß leider nicht mehr, wie in die Grenzen für das Intervall berechne, kann mir jemand helfen?

Comments

f(x)=0,5x^2-2
g(x)=-0,5x+1

0,5x^2-2=-0,5x+1

0,5x^2+0,5x-3=0

0,5x^2+0,5x=3|*2

x^2+1*x=6

(x+\( \frac{1}{2} \))^2=6+(\( \frac{1}{2} \))^2=6,25|\( \sqrt{} \)

1.)x+\( \frac{1}{2} \)=2,5

x₁=2

2.)x+\( \frac{1}{2} \)=-2,5

x₂=-3

Answer 1

Schnittpunkte von f und g bedeuten, die Graphen schneiden sich, d.h. haben bei den gesuchten x-Werten denselben y-Wert. Setze die Funktionen gleich und löse die Gleichung nach x auf. Es gibt 2 Lösungen.

Dann integriere die Differenz der beiden Funktionen vom kleineren Schnittpunkt bis zum größeren Schnittpunkt.

Comments

Vielen Danke:)

---

Ich habe jetzt 2;-3 raus. Muss ich diese jetzt in die Grenzen von 2;0 und 0;-3 trennen oder anderes?

---

Ich denke, der zweite Abschnitt meiner Antwort beantwortet Deine Frage?

---

"Ich habe jetzt 2;-3 raus. Muss ich diese jetzt in die Grenzen von 2;0 und 0;-3 trennen oder anderes?"

Ich verschiebe mal die beiden Graphen von

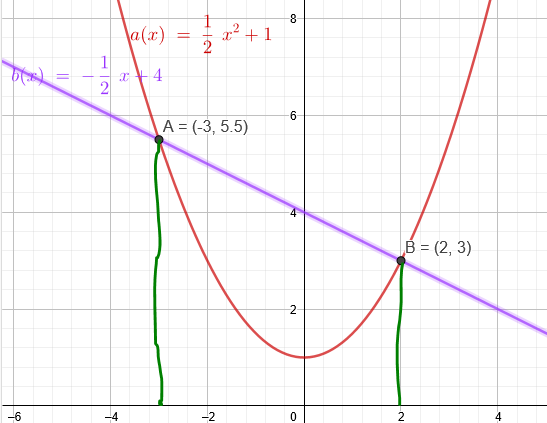
f(x)=0,5x^2-2  und g(x)=-0,5x+1 um 3 Einheiten nach oben:

a(x)=0,5x^2+1 und b(x)=-0,5x+4

Jetzt siehst du, dass die gesuchte Fläche mit A=\( \int\limits_{-3}^{2} \)(b(x)-a(x))*dx

zu berechnen ist.

---

Tarzans grüne Lianen haben sich irgendwie in meine Antwort verirrt.

Answer 2

Schnittpunkte (=Integrationsgrenzen) findet man durch Gleichsetzen: \( \frac{x^2}{2} \)-2= - \( \frac{x}{2} \)+1 ist eine quadratische Gleichung mit den Lösungen x₁ = - 3 und x₂ = 2.

Answer 3

Differenzfunktion

d(x) = f(x) - g(x) = 0.5·x^2 + 0.5·x - 3

Schnittstellen

d(x) = 0.5·x^2 + 0.5·x - 3 = 0 --> x = -3 ∨ x = 2

Stammfunktion

D(x) = 1/6·x^3 + 1/4·x^2 - 3·x

Fläche

A = ∫ (-3 bis 2) d(x) dx = D(2) - D(-3) = - 11/3 - 27/4 = - 125/12 = -10.42

Die Fläche beträgt etwa 10.42 FE.