Berechnen Sie die Integrale durch partielle Integration: Wo liegt der Fehler?

Question

Folgende Aufgabe:

Berechnen Sie die Integrale durch partielle Integration

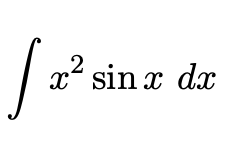
Text erkannt:

$\int x^{2} \sin x d x$

Meine Lösung stimmt jedoch nicht mit der Musterlösung überein... wo liegt der Fehler?

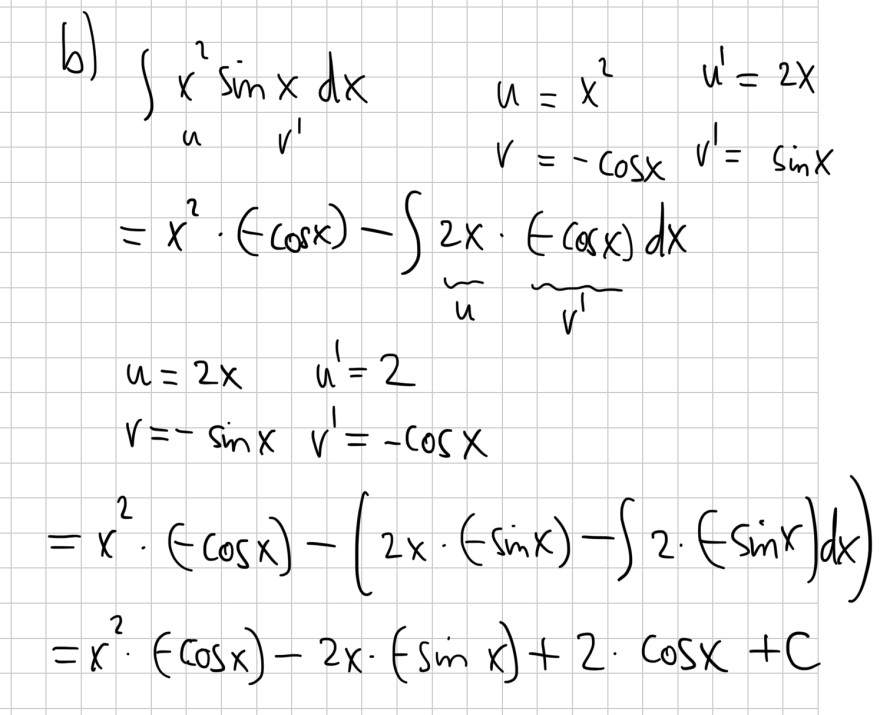
Text erkannt:

b) $\begin{aligned} & \int x^{2} \sin x d x \quad u=x^{2} \quad u^{\prime}=2 x \\ & u \quad v^{\prime} \\=& x^{2} \cdot(-\cos x)-\int \limits_{v}=-\cos x v^{\prime}=\sin x \\ & u(-\cos x) d x \\ & u=2 x \quad u^{\prime}=2 \\ & v=-\sin x v^{\prime}=-\cos x \\=& x^{2} \cdot(-\cos x)-\left(2 x \cdot(-\sin x)-\int 2 \cdot(-\sin x) d x\right) \\=& x^{2} \cdot(-\cos x)-2 x \cdot(-\sin x)+2 \cdot \cos x+C \end{aligned}$

Musterlösung:

2x*sin(x)−(x² −2)*cos(x)+C

Comments

Wo siehst Du einen Unterschied zur Musterlösung?

---

Meine Lösung sieht doch komplett anders aus?

---

Ich sehe keinen Unterschied

Answer 1

Aloha :)

$$I=\int \underbrace{x^2}_{=u}\cdot\underbrace{\sin x}_{=v'}\,dx=\underbrace{x^2}_{=u}\cdot\underbrace{(-\cos x)}_{=v}-\int \underbrace{2x}_{=u'}\cdot\underbrace{(-\cos x)}_{=v}\,dx$$$$\phantom{I}=-x^2\cos x+2\int \underbrace{x}_{=u}\cdot\underbrace{\cos x}_{=v'}\,dx=-x^2\cos x+2\left(\underbrace{x}_{=u}\cdot\underbrace{\sin x}_{=v}-\int \underbrace{1}_{=u'}\cdot\underbrace{\sin x}_{=v}\,dx\right)$$$$\phantom{I}=-x^2\cos x+2x\sin x-2\int\sin x\,dx=-x^2\cos x+2x\sin x+2\cos x+\text{const}$$$$\phantom{I}=(2-x^2)\cos x+2x\sin x+\text{const}$$