Aufgabe:
Zwei Streckenlängen b,c ∈ R mit b > c > 0 stehen im Verhältnis des Goldenen Schnitts, wenn das Verhältnis a = b/c der längeren Strecke b zur kürzeren Strecke c gleich dem Verhältnis a′ = (b + c)/b der Summe der beiden Strecken zur längeren Strecke ist.
Wir beweisen mit Hilfe komplexer Zahlen, dass die Diagonalen und die Seiten eines regelmä- ßigen Fünfecks im Verhältnis des Goldenen Schnitts stehen.
(c) Zeigen Sie, dass x und ζ aus (b) die folgenden Gleichungen erfüllen:
1 + ζ + ζ^2 + ζ^3 + ζ^4 = 0
Problem/Ansatz:
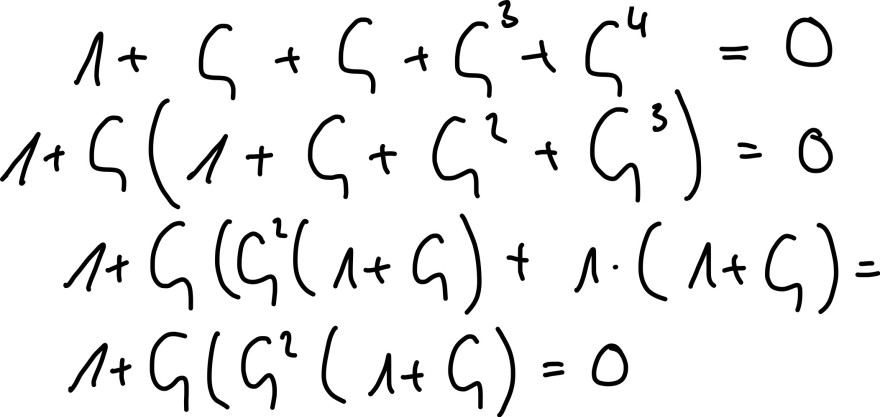
Text erkannt:
\( 1+G+G+G^{3}+G^{4}=0 \)
\( 1+G\left(1+C_{1}+C_{1}^{2}+C^{3}\right)=0 \)
\( 1+G\left(C_{1}^{2}(1+G)+1 \cdot(1+C)=\right. \)
\( 1+G\left(G^{2}\left(1+C_{1}\right)=0\right. \)
Stimmt der Ansatz? Wie mache ich jetzt weiter?