Aufgrund meines Modells würde ich mich auf die maximale Mantellinie auf dem Grundkreis konzentrieren
das x ist die y-Koordinate von E=(0,x,sqrt(R^2-x^2)), Kugelradius R=1
\(r \, := \, \frac{\sqrt{R^{2} + R \; x}}{\sqrt{2}}\)
\(h \, := \, \sqrt{2} \; \sqrt{R^{2} - R \; x}\)
Vmax(x) liegt dann bei x=1/3
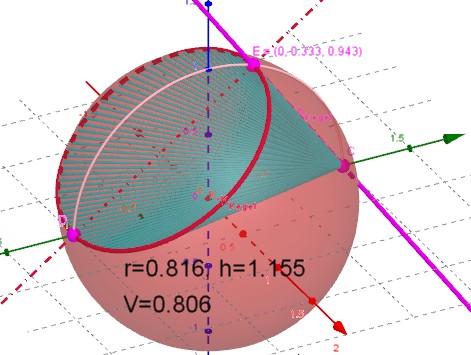
Wenn DU den Grundkreis anders anstellen willst müsste man neu verhandeln...