Aufgabe:
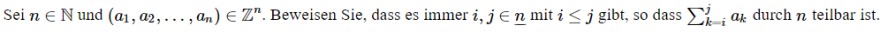
Text erkannt:
Sei \( n \in \mathbb{N} \) und \( \left(a_{1}, a_{2}, \ldots, a_{n}\right) \in \mathbb{Z}^{n} . \) Beweisen Sie, dass es immer \( i, j \in \underline{n} \) mit \( i \leq j \) gibt, so dass \( \sum \limits_{k-i}^{j} a_{k} \) durch \( n \) teilbar ist.
Problem/Ansatz:
Hi, ich komme bei der Aufgabe leider nicht weiter.
Hat jemand eine passende Lösung parat?
Bin für jede Hilfe dankbar!