Aufgabe:
Warum gilt folgendes:
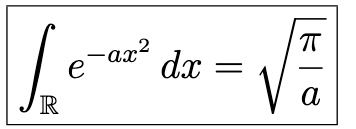
fuer a > 0
Problem/Ansatz:
Den Beweis davon verstehe ich, allerdings sehe ich nicht meinen Fehler bei folgenden vorgehen:
Einfach das e^-a aus den Integral rausziehen und das "normale Gauß Integral loesen. Das Ergebniss waere dann:
e^-a * sqrt(pi)
$$\int \limits_{-\infty}^{\infty}e^{-a \cdot x^ {2}} = e^{-a}\int \limits_{-\infty}^{\infty}e^{x^ {2}} =e^{-a} \sqrt{\pi}$$