Aufgabe:
Sei \( \mathbb{K} \) ein Körper und \( V \) ein endlich dimensionaler \( \mathbb{K} \)-Vektorraum. Seien \( U_{1}, U_{2}, U_{3} \subset V \) Unterräume von \( V \).
i) Zeigen Sie, dass die Formel
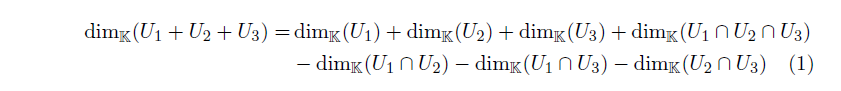
Text erkannt:
\( \begin{aligned} \operatorname{dim}_{\mathbb{K}}\left(U_{1}+U_{2}+U_{3}\right)=& \operatorname{dim}_{\mathbb{K}}\left(U_{1}\right)+\operatorname{dim}_{\mathbb{K}}\left(U_{2}\right)+\operatorname{dim}_{\mathbb{K}}\left(U_{3}\right)+\operatorname{dim}_{\mathbb{K}}\left(U_{1} \cap U_{2} \cap U_{3}\right) \\ &-\operatorname{dim}_{\mathbb{K}}\left(U_{1} \cap U_{2}\right)-\operatorname{dim}_{\mathbb{K}}\left(U_{1} \cap U_{3}\right)-\operatorname{dim}_{\mathbb{K}}\left(U_{2} \cap U_{3}\right) \end{aligned} \)
im Allgemeinen falsch ist. Zeigen Sie, dass für \( U_{1} \subset U_{3} \) die Formel (1) wahr ist \( { }^{1} \).
ii) Zeigen \( \operatorname{Sie} \operatorname{dim}_{\mathbb{K}}\left(U_{1}+U_{2}+U_{3}\right) \leq \operatorname{dim}_{\mathbb{K}}\left(U_{1}\right)+\operatorname{dim}_{\mathbb{K}}\left(U_{2}\right)+\operatorname{dim}_{\mathbb{K}}\left(U_{3}\right) \).
iii) Sei nun \( \operatorname{dim}_{\mathrm{K}}(V)=n \geq 3 \). Zeigen Sie mithilfe der Dimensionsformel, dass aus \( \operatorname{dim}_{\mathrm{K}}\left(U_{1}\right)= \) \( \operatorname{dim}_{\mathbb{K}}\left(U_{2}\right)=\operatorname{dim}_{\mathbb{K}}\left(U_{3}\right)=n-1 \) die Aussage \( \operatorname{dim}_{\mathbb{K}}\left(U_{1} \cap U_{2} \cap U_{3}\right) \geq n-3 \) folgt.
Problem/Ansatz: Fur i dachte ich, dass man dazu einen Gegebeispeil verwenden konnte, aber ansonsten bin ich leider nicht weitergekommen.