Kegelschnitte Ellipse Hyperbel

Question

Hallo!

Kann mir bitte jemand mit folgendem Beispiel helfen?

Eine Ellipse hat den Hauptscheitel A = (3 die Wurzel vom n 2|0) und führt durch den Punkt P = (3|2).

 1) Bestimme die Gleichung der Ellipse und die Glei- chung der gleichseitigen Hyperbel, die ebenfalls durch den Punkt P führt.

 2) Die Asymptoten der Hyperbel schließen mit der Tangente im Punkt P an die Hyperbel ein Dreieck ein. Berechne dessen Flächeninhalt.

Danke sehr im Voraus

Comments

hallo!

Ich bessere es aus, der Hauptscheitel ist (3$\sqrt{2}$|0)

Kann mir bitte jemand mit dem Lösen der Aufgabe helfen?

Vielen Dank im Voraus

Answer 1

Hallo

wo der Hauptscheitel liegt kann ich nicht entziffern stattdessen schreib ich a

du hast x²/a²+y²/b²=1 trage dein richtiges a ein, dann setze den Punkt = ein um b zu bestimmen.

Dann Hyperbel x²/c²-y²/c²=1  P eintragen. c bestimmen.

es kann auch y²/c²-x²/c²)=1 sein

Asymptoten in jeden Fall y=x

Tangente an die Hyperbel kannst du sicher mit Asymptote schneiden

da 2 Geraden nie ein Dreieck bilden  muss wohl noch ne Achse dazukommen ?

Gruß lul

Comments

Kann sein , dass bei Ellipse b= 8 und bei Hyperbel b=-8 rauskommt ?

Ich verstehe nicht ganz wie ich die nr. 2 lösen soll

---

Hallo

für b der Ellipse hast du b²=8 NICHT b=8

für die Hyperbel ist c=-8 oder b=-8 falsch. Hast du da nicht eine gleichseitige Hyperbel genommen, also beide Achsen gleich, die hatte ich dir hingeschrieben.

Was an 2) kannst du nicht? die Tangente in (3,2) an die Ellipse? x*3/a²+y*2/b²=1 die mit der Asymptote schneiden ? mit der x-Achse schneiden? Fläche eines Dreiecks ausrechnen? Du musst schon sagen, was dir fehlt. Schreib nicht einfach Ergebnisse wie b=-8 sondern deinen Rechenweg

Kontrolle: die Fläche ist 3*2,4FE

Gruß lul

Answer 2

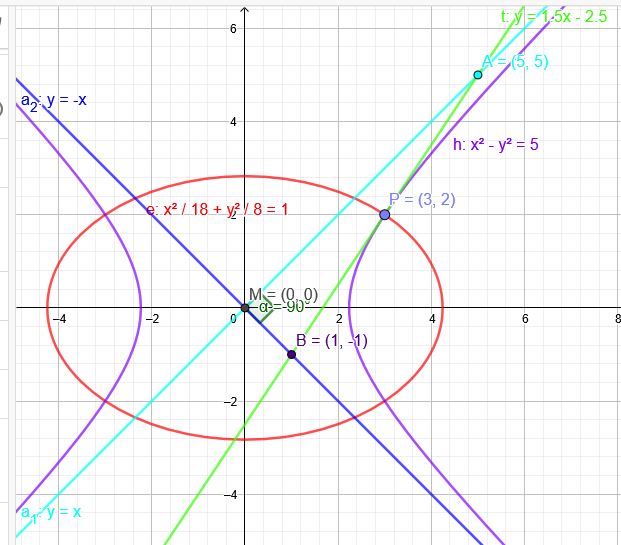
Eine Ellipse hat den Hauptscheitel  A$(3\sqrt{2}|0)$ und führt durch den Punkt  P$(3|2)$.

1) Bestimme die Gleichung der Ellipse und die Gleichung der gleichseitigen Hyperbel, die ebenfalls durch den Punkt P führt.

$e: \frac{x^2}{(3\sqrt{2})^{2}}+\frac{y^2}{b^2}=1$

$e: \frac{x^2}{18}+\frac{y^2}{b^2}=1$

P$(3|2)$

$\frac{9}{18}+\frac{4}{b^2}=1$→$0,5+\frac{4}{b^2}=1$

$\frac{4}{b^2}=0,5$

$b^2=8$

$e: \frac{x^2}{18}+\frac{y^2}{8}=1$

gleichseitige Hyperbel:

$h: \frac{x^2}{a^2}-\frac{y^2}{a^2}=1$

$h: x^2-y^2=a^2$

P$(3|2)$                $a^2=5$

$h: x^2-y^2=5$

2) Die Asymptoten der Hyperbel schließen mit der Tangente im Punkt P $(3|2)$an die Hyperbel ein Dreieck ein. Berechne dessen Flächeninhalt.

Bei einer gleichseitige Hyperbel müssen die Asymptoten senkrecht aufeinander stehen:
$y=x$  und $y=-x$
Tangente an die Hyperbel im Punkt  P$(3|2)$

$h: x^2-y^2=5$ muss nun nach $y$ aufgelöst und abgeleitet werden.

$y=±\sqrt{x^2-5}$ 
Hier benötigt man nur den positiven Teil wegen P$(\red{3}|2)$

$y=\sqrt{x^2-5}$   →   $y'=\frac{2x}{2\sqrt{x^2-5}}=\frac{x}{\sqrt{x^2-5}}$

$y'(\red{3})=\frac{3}{\sqrt{9-5}}=1,5$

Für die Tangente verwende ich die Punkt-Steigungsform der Geraden.

$\frac{y-2}{x-3}=1,5$

$y=1,5(x-3)+2=1,5x-2,5$  Schnitt mit den beiden Asymptoten:

1.)     $1,5x-2,5=x$    $x=5$       $y=5$      A$(5|5)$

2.)    $1,5x-2,5=-x$    $x=1$      $y=-1$      B$(1|-1)$

Fläche des rechtwinkligen Dreiecks

$\overline{AM}= \sqrt{5^2+5^2}=5\sqrt{2}$

$\overline{BM}= \sqrt{1^2+(-1)^2}=\sqrt{2}$

$A=0,5 \cdot 5\sqrt{2} \cdot \sqrt{2}=5$FE