a) Mit l´Hospital:
\(\lim\limits_{x->0}\frac{(1+x)^{3}-(1+3x)}{x^{2}+4x^{3}} \)=\(\lim\limits_{x->0}\frac{3*(1+x)^{2}-3}{2x+12x^{2}} \)=\(\lim\limits_{x->0}\frac{6*(1+x)}{2+24x} \)=3
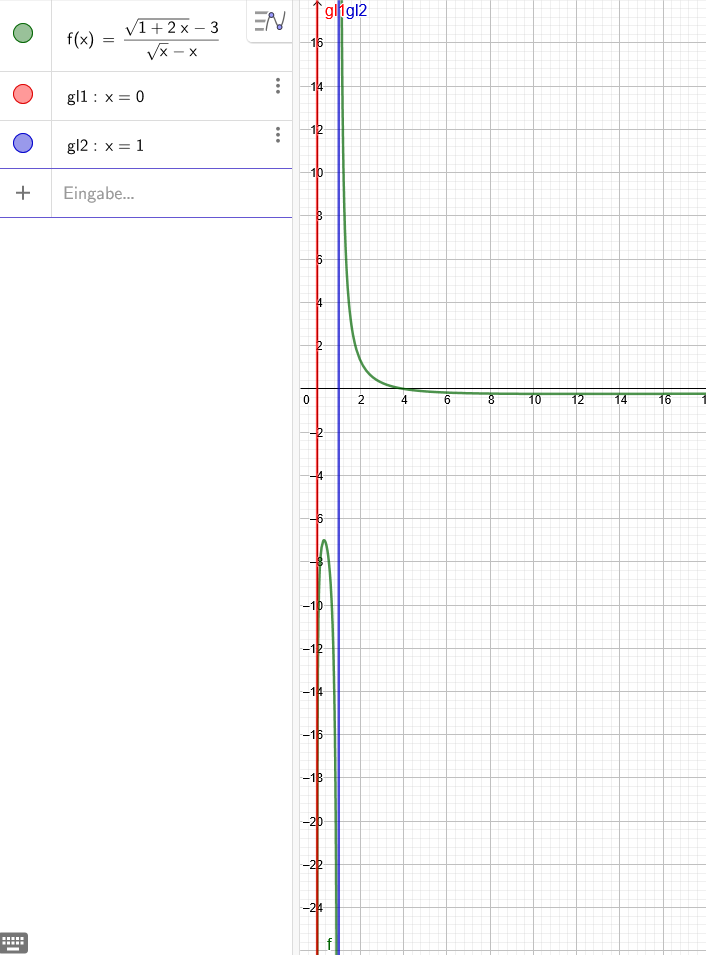
b)\(\lim\limits_{x->4}\frac{\sqrt{1+2x}-3}{\sqrt{x}-x} \)=0
Polstellen:
\( \sqrt{x} \) -x=0
\( \sqrt{x} \)=x|^2
x=\( x^{2} \)
\( x^{2} \)-x=0
x*(x-1)=0
x₁=0 (in rot)
x₂=1 (in blau)
Ist nicht eher so die Aufgabe gestellt ?
1.) \(\lim\limits_{x->0+}\frac{\sqrt{1+2x}-3}{\sqrt{x}-x} \)→-∞
2.) \(\lim\limits_{x->1+}\frac{\sqrt{1+2x}-3}{\sqrt{x}-x} \)→∞
\(\lim\limits_{x->1-}\frac{\sqrt{1+2x}-3}{\sqrt{x}-x} \)→-∞