a) Mit l´Hospital:
x−>0limx2+4x3(1+x)3−(1+3x)=x−>0lim2x+12x23∗(1+x)2−3=x−>0lim2+24x6∗(1+x)=3
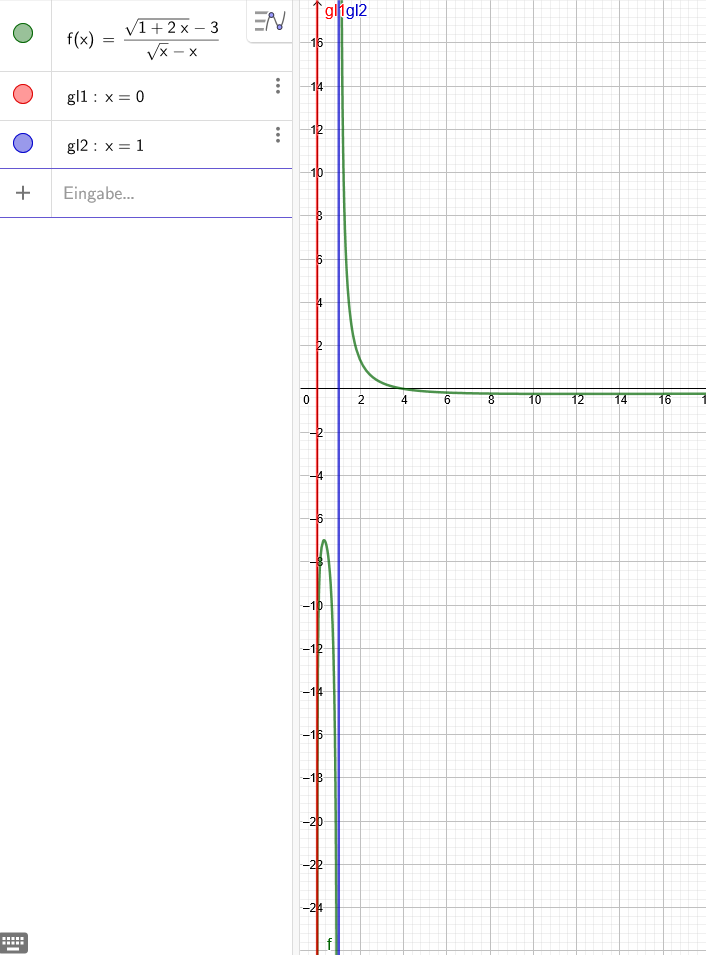
b)x−>4limx−x1+2x−3=0
Polstellen:
x -x=0
x=x|^2
x=x2
x2-x=0
x*(x-1)=0
x₁=0 (in rot)
x₂=1 (in blau)
Ist nicht eher so die Aufgabe gestellt ?
1.) x−>0+limx−x1+2x−3→-∞
2.) x−>1+limx−x1+2x−3→∞
x−>1−limx−x1+2x−3→-∞