wenn Du eine Geradengleichung aufstellst wie
g: x = (2/4/5) + t(1/1/-7)
dann ist der erste Teil, der "Stützvektor" sozusagen ein Punkt im Raum und der zweite ist der "Richtungsvektor", der die Richtung von diesem Punkt "weg" bezeichnet.
Stellen wir uns das Ganze mal im zweidimensionalen Raum vor mit dem
Stützvektor A(2|4) und dem Richtungsvektor (1|1):
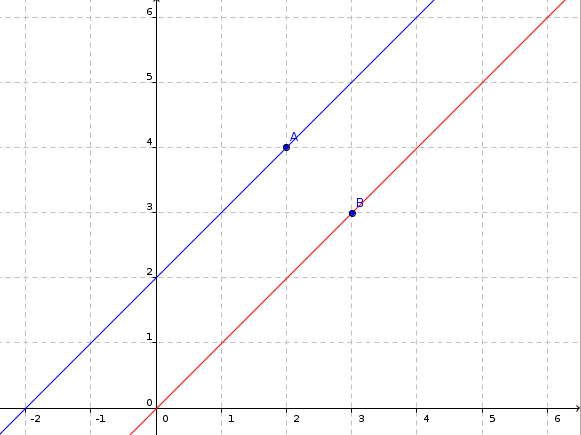
Wie Du siehst, habe ich an A den Richtungsvektor "angelegt", so dass sich die blaue Gerade ergab.
Nehme ich aber den gleichen Richtungsvektor, aber einen anderen Stützvektor B, erhalte ich die rote Gerade, die parallel zur blauen ist.
Es kommt also im 2D als auch im 3D darauf an, dass man einen oder mehrere (bei Ebenen) Richtungsvektoren an einen bestimmten Stützvektor anhängt, um die Gerade oder Ebene eindeutig zu bestimmen.
Besten Gruß