Und zwar gab es den Hinweis, dass man die ii und iii mithilfe der Substituion einer Hyperbelfunktion lösen kann. Jedoch sehe ich hier nicht, wie ich dies hier tun kann und es ähnelt mir bei ii eher nach der Ableitung von arctanx mit Wurzel im Nenner. Ich sehe nicht, wie ich hier die Hyperbelfunktionen mit den ganzen e einbringen soll.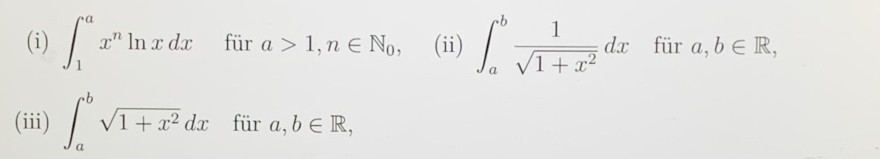
Text erkannt:
(i) \( \int \limits_{1}^{a} x^{n} \ln x d x \quad \) für \( a>1, n \in \mathbb{N}_{0} \),
(ii) \( \int \limits_{a}^{b} \frac{1}{\sqrt{1+x^{2}}} d x \quad \) für \( a, b \in \mathbb{R} \),
(iii) \( \int \limits_{a}^{b} \sqrt{1+x^{2}} d x \quad \) für \( a, b \in \mathbb{R} \),