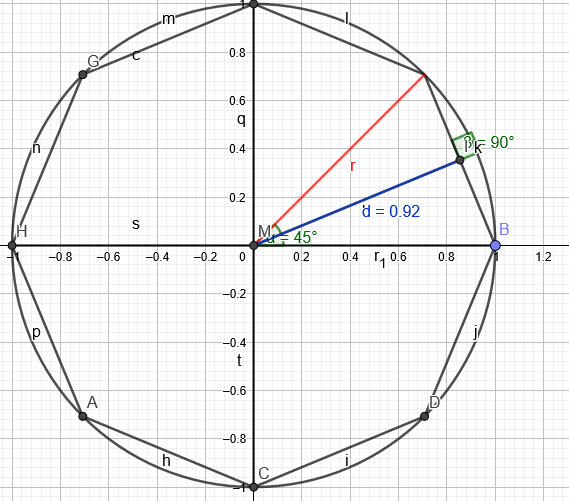
Eine Dreieckfläche:
\( \frac{45°}{2} \)=22,5°
sin(22,5°)=\( \frac{x}{r} \)=\( \frac{x}{1} \)=x , wobei x die halbe Sehne ist.
x≈0,38
Höhe des Dreiecks ist cos(22,5°)≈0,92
A Dreieck=sin(22,5°)*cos(22,5°)=0,3536
Gesamtfläche: 0,3536*8=2,8288\( m^{2} \)
AKreis=π