Zeigen Sie, dass die linke Seitenfläche DAEH des Tempels ein Trapez ist.

Question

Hi Leute,

Ich bräuchte etwas Hilfe bei folgender Aufgabe:

PYRAMIDE UND TEMPEL

Gegeben ist ein Tempel, der die Form eines quadratischen Pyramidenstumpfes mit den Ecken A (8|0|0), B(0|8|0), C(-8|0|0), D(0|-8|0), E(4|0|6), F(0|4|6), G(-4|0|6) und H (0|-4|6) besitzt (s.Abb). Dabei ist 1 LE = 10m.

a)  Zeigen Sie, dass die linke Seitenfläche DAEH des Tempels ein Trapez ist.

b)  Bestimmen Sie die Höhe des Trapezes DAEH und berechnen sie seinen Flächeninhalt.

c)  Bestimmen Sie eine Parameter- und eine Koordinatengleichung der Ebene e, in der die vordere Seitenfläche ABFE des Tempels liegt.

d)  Bestimmen Sie den Schnittwinkel der Ebene e mit dem Erdboden.

e)  Der Tempel hat die Form eines quadratischen Pyramidenstumpfes. Berechnen Sie die Koordinaten der Spitze Z der zugehörigen Gesamtpyramide (s.Abb).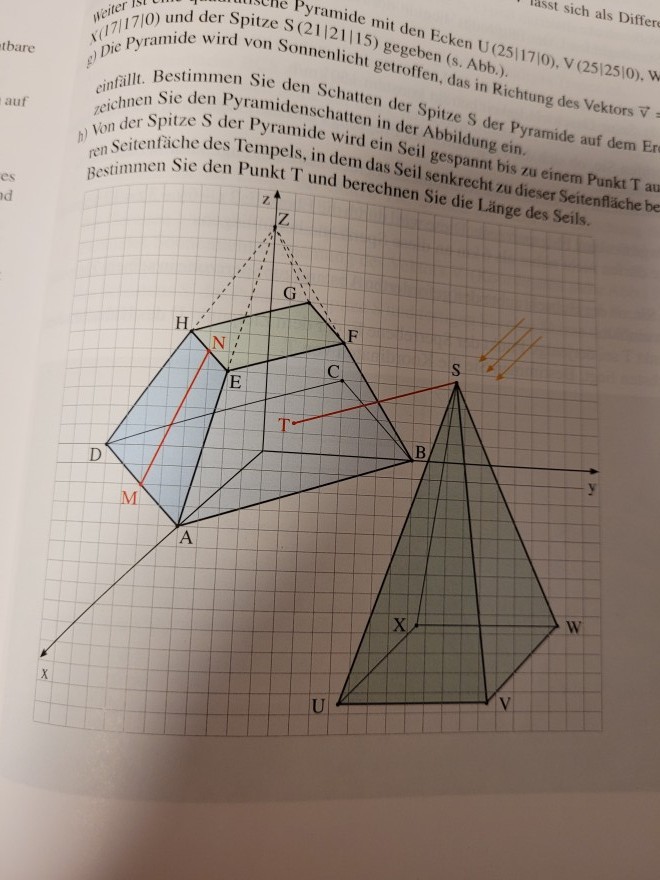

f)  Bestimmen sie das Volumen V des Tempels. Hinweis: V lässt sich als Differenz zweier Pyramidenvolumina darstellen.

Weiter ist eine quadratische Pyramide mit den Ecken U(25|17|0), V(25|25|0), W(17|25|0), X(17|17|0) und der Spitze S(21|21|15) gegeben.

g) Die Pyramide wird von Sonnenlicht getroffen, das in Richtung des Vektors v =(-1 -3 -3) einfällt. Bestimmen Sie den Schatten der Spitze S der Pyramide auf dem Erdboden und zeichnen Sie den Pyramidenschatten in der Abbildung ein.

h) Von der Spitze S der Pyramide wird ein Seil gespannt bis zu einem Punkt T auf der vorderen Seitenfläche des Tempels, in dem das Seil senkrecht zu dieser Seitenfläche befestigt wird. Bestimmen Sie den Punkt T und berechnen Sie die Länge des Seils.

Ich wäre euch sehr dankbar, wenn ihr mir helfen könntet.

Answer 1

a) war gefragt:  Berechne die Vektoren DA und EH

(durch A-D bzw H-E) und zeige:

-2 EH = DA, also sind die beiden Vielfache voneinader.

==>  Die Strecken sind parallel

==>  Das Viereck ist ein Trapez.

Comments

Ok, vielen Dank. Das habe ich auch noch hingekriegt. Bei mir scheitert es erst ab d

---

d) Aus der Koordinatengleichung von E kannst du einen

Normalenvektor ablesen.

Berechne den Winkel zwischen dem und \( \begin{pmatrix} 0\\0\\1 \end{pmatrix}\).

e) Schneide z.B. die Geraden AE und DH.

f) Da hast du doch einen Tipp !

g) Gerade durch S mit Richtungsvektor \( \begin{pmatrix} -1\\-3\\-3 \end{pmatrix}\) schneidet die xy-Ebene bei (16/6/0). Das ist der

Schattenpunkt der Spitze.

h)  Nimm den Normalenvektor aus d)  als Richtungsvektor einer

Geraden durch den Punkt S und schneide diese mit der Ebene.

Dann hast du T.

---

Ok Dankeschön. Aber wieso 0 0 1

---

Das ist der Normalenvektor der xy-Ebene (Erdboden).

---

Hallo ich habe leider auch meine Schwierigkeiten mit der Aufgabe.. Hätten Sie eventuell noch Tipps oder Lösungsansätze für b und c? Bei b weiß ich nicht wie man h berechnet und bei c weiß ich nicht wie man aus 4 Punkten erstmal eine Gleichung aufstellt.. ich hatte das immer nur mit 3 Punkten. Könnten Sie mir da weiter helfen?

---

Bei b weiß ich nicht wie man h berechnet ...

Die Geraden durch \(AD\) und \(EH\) verlaufen parallel. Im allgemeinen Fall reicht es also aus, den Abstand eines Punktes der einen Gerade - z.B. \(E\) - zur anderen Geraden - dann \(g_{AD}\) - zu berechnen. (1.Möglichkeit)

In diesem konkreten Fall sind \(M\) und \(N\) die Mittelpunkte der Strecken \(AD\) und  \(EH\) und \(MN\) ist auch eine Höhe des Trapez, wg. der Symmetrie. Berechne also den Abstand \(|MN|\). (2.Möglichkeit)

Man kann es aber auch in der Zeichnung 'sehen' (3.Möglichkeit):$$|MN| = \sqrt{(2\sqrt{2})^2 + 6^2} = \sqrt{44}$$

... und bei c weiß ich nicht wie man aus 4 Punkten erstmal eine Gleichung aufstellt.. ich hatte das immer nur mit 3 Punkten.

Da \(AB\) und \(EF\) parallel verlaufen (überprüfe das!), lasse einen der vier Punkte weg und bestimme die Ebene aus den drei verbleibenden.

Tipp: mache einen neue Frage hier in der Mathelounge auf und frage konkret nach den Aufgaben b) und c). Und erwähne dabei noch, dass dies hier nicht gelöst worden ist.

Answer 2

A (8|0|0), B(0|8|0), C(-8|0|0), D(0|-8|0), E(4|0|6), F(0|4|6), G(-4|0|6) und H (0|-4|6)

AD = D - A = [-8, -8, 0]

EH = H - E = [-4, -4, 0]

Damit sind AD und EH parallel und AD ist doppelt so lang wie EH. Da man sieht das die 4 Punkte nicht auf einer Geraden liegen ist das Viereck damit ein Trapez.

Comments

Vielen Dank. Das habe ich geschafft. Bei mir happert es ab d).