gebrochen rational funktion

Question

Aufgabe:

c) Die Geraden mit den Gleichungen x = -3, und y=x-3 sowie der Graph von g und die x-Achse begrenzen ein Flächenstück. Markieren Sie das gesuchte Flächenstück im angefügten Ausschnitt des Koordinatensystems und berechnen Sie dessen Inhalt.
g(x)= $\frac{x^{2}-5}{x+3}$   beachten dass g(x)  eine gebrochene rationale Funktion ist

Answer 1

Inhalt der gesuchten Fläche ist

        $\int_{-\sqrt{5}}^{\sqrt{5}} g(x)\mathrm{dx} - \int_{-3}^3 (x-3)\mathrm{d}x$.

Die Integrationsgrenzen $-\sqrt{5}$ und $\sqrt{5}$ sind die Nullstellen von $g$ und die Integrationsgrenze $3$ ist die Nullstelle von $y=x-3$.

Comments

Sehr schön, danke Bruder

Answer 2

Vom Duplikat:

Titel: Fläche zwischen 3 Funktionen berechnen

Stichworte: gebrochenrationale-funktionen

Guten Tag Leute,

Wie Kann ich diese Aufgabe lösen, was soll ich genau machen, mit welchen Ansatz muss ich solche Aufgaben lösen, Integral Rechnung?

Text erkannt:

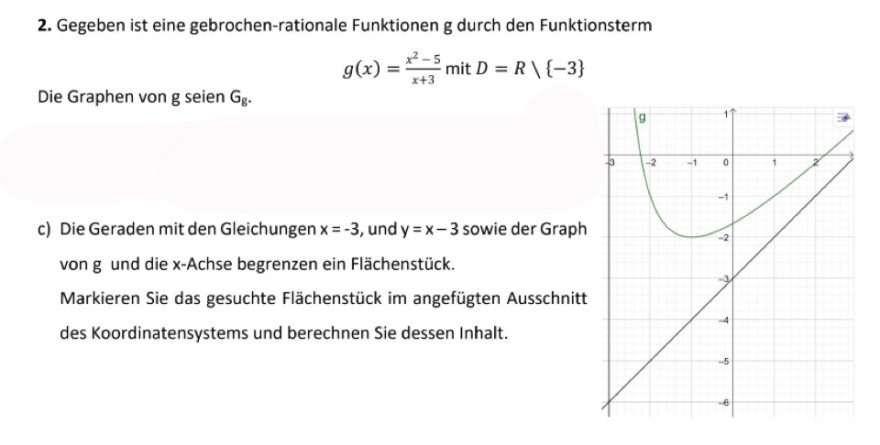
2. Gegeben ist eine gebrochen-rationale Funktionen g durch den Funktionsterm
$g(x)=\frac{x^{2}-5}{x+3} \text { mit } D=R \backslash\{-3\}$
Die Graphen von g seien $\mathrm{G}_{\mathrm{g}}$.
Fhungen $x=-3$, und $y=x-3$ sowie der Graph
und berechnen Sie dessen Inhalt.

Aufgabe:

…

Problem/Ansatz:

Comments

Schau mal hier:

https://www.mathelounge.de/921952/gebrochen-rational-funktion

---

Danke schön the kingf, gut das du die Frage gestellt hast

---

In der verlinkten Frage ist nur noch c) vorhanden. Die Vorarbeiten aus a) und b) somit überflüssig?

---

Hi Lu, ich hab’ a+b gelöst

Vielen lieben Dank