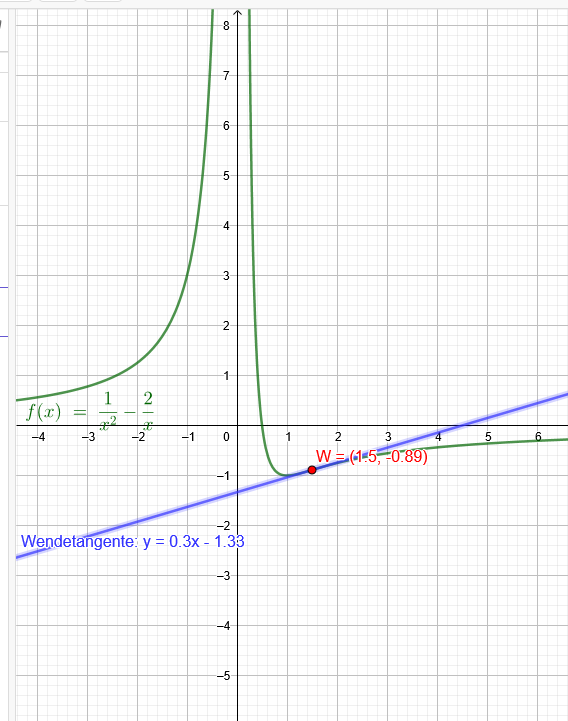
f(x) = \( \frac{1}{x^2} \) - \( \frac{2}{x} \)
f(x)=\( x^{-2} \)-2*\( x^{-1} \)
f´(x)=-2*\( x^{-2-1} \)-2*(-1)*\( x^{-1-1} \)
f´(x)=-2*\( x^{-3} \)+2*\( x^{-2} \)
f´´(x)=-2*(-3)\( x^{-3-1} \)+2*(-2)*\( x^{-2-1} \)
f´´(x)=6*\( x^{-4} \)-4*\( x^{-3} \)
Wendepunkt:
6*\( x^{-4} \)-4*\( x^{-3} \)=0 |*\( x^{4} \)
6-4x=0
x=\( \frac{3}{2} \) f(\( \frac{3}{2} \))=...
Steigung der Wendetangente:
f´(\( \frac{3}{2} \))=...
Tangente mit der Punkt-Steigungsform der Geraden bestimmen.