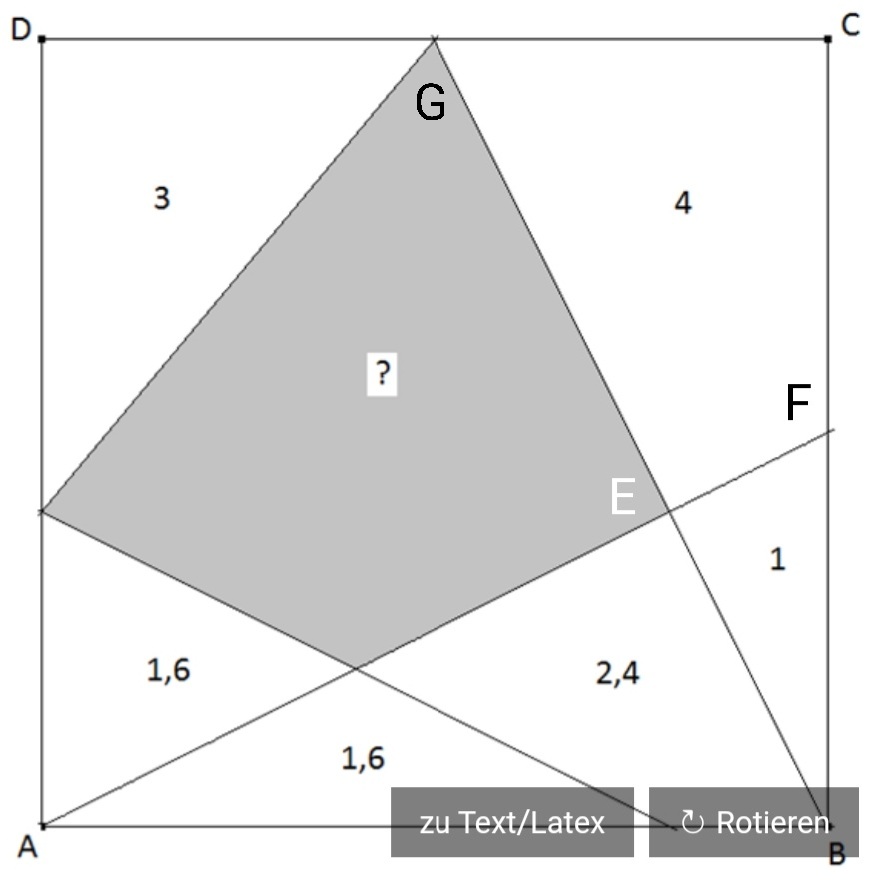
Die Dreiecke ABF und BCG sind kongruent, da die Seiten des Quadrats gleichlang sind und in den Ecken rechte Winkel sind. Da die Flächeninhalte gleich sind, müssen auch die Seiten BF und CG gleichlang sein.
Bei E schneiden sich die Strecken AF und BG orthogonal, da die beiden kongruenten Dreiecke durch eine 90°-Drehung aufeinander abgebildet werden können.
EB ist daher die Höhe im Dreieck ABF.
Da das Dreieck EAB viermal so groß ist wie das Dreieck EBF gilt:
AE=4•EF
Mit dem Höhensatz für das Dreieck ABF erhält man
EB²=AE•EF=4•EF² → EB=2•EF
Da die Dreiecke EBF und GBC ähnlich sind, ist CB=2•GC.
Damit ist G der Mittelpunkt der Seite CD und der Flächeninhalt des Dreiecks BCG ein Viertel des Quadrats, dessen Flächeninhalt 20 beträgt.
Subtraktion der Summe der gegebenen Flächeninhalte von 20 ergibt 6,4FE für das graue Viereck.
:-)