Sei I ⊂ ℝ ein nichttriviales Intervall und a ∈ I.
Man betrachte die Funktionen f, g : I \ {a} → ℝ. Es gelte
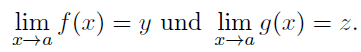
Ich soll nun zeigen dass dann
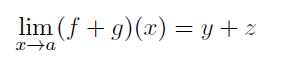
gilt.
Dazu darf ich nur folgende Definition verwenden:
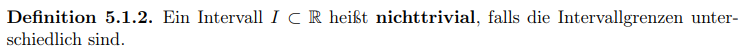
Ich verstehe nicht wie ich das "nur" mit dieser Definition zeigen soll.