c) \(f(x)= x^5+x^3\)
\(f´(x)= 5x^4+3x^2\)
\( 5x^4+3x^2=0→x^2*(5x^2+3)=0→x^2=0\) doppelte Nullstelle
\(5x^2=-3→ k.L. in ℝ\)
\(f´´(x)= 20x^3+6x\)
\(f´´(0)= 0 \) Somit kein Extremwert, aber Sattelpunkt \(f´´´(x)= 60x^2+6\) \(f´´´(0)= 6\)
\(20x^3+6x=0→x*(20x^2+6)→x=0;f(0)=0 \) Wendepunkt
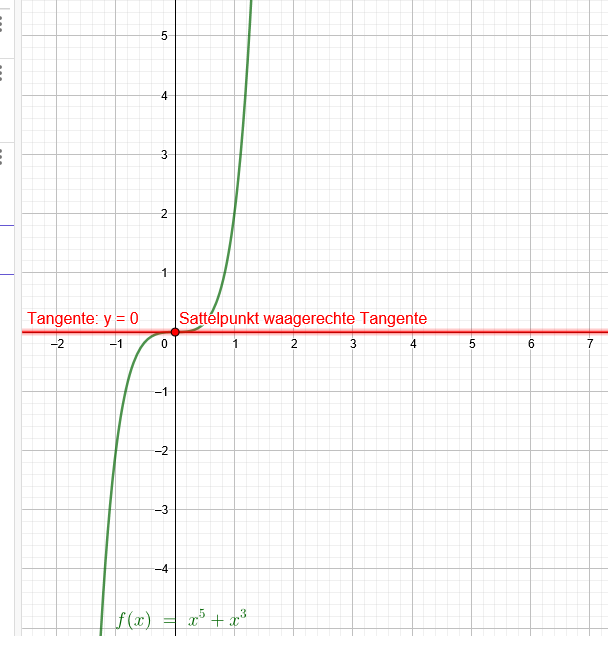
Text erkannt:
Tangente: \( \mathrm{y}=0 \quad \) Sattelpunkt waagerechte Tangente