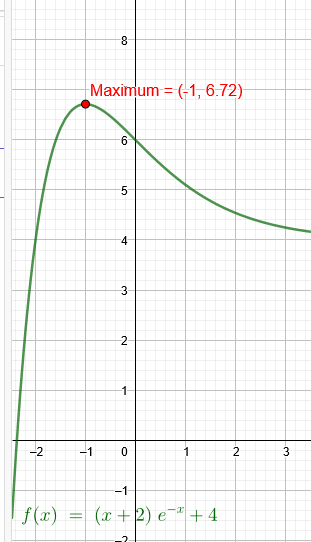
\(f(x)=(x+2)•e^{-x}+4\)
\(f´(x)=1•e^{-x}+(x+2)*e^{-x}•(-1)\)
\(f´(x)=e^{-x}-(x+2)*e^{-x}\)
\(e^{-x}-(x+2)*e^{-x}=0\)
\(e^{-x}*[1-x-2)]=0\)
Satz vom Nullprodukt anwenden:
\(e^{-x}=0\) kann nicht 0 werden
\([1-x-2]=0→x=-1→f(-1)=(-1+2)•e^{1}+4=6,72\)
Art des Extremwertes:
\(f´´(x)=e^{-x}•(-1)•[-1-x)+e^{-x}•(-1)]\)
\(f´´(-1)=e^{1}•(-1)<0 Maximum]\)