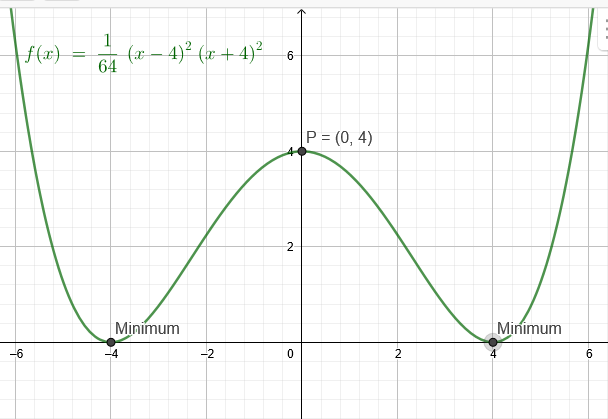
"Eine zur y-Achse symmetrischer Graph einer Funktion 4.Grades verläuft durch den Punkt P(0|4) und hat in T(4|0) ein Minimum. Wie lautet die Funktionsgleichung?"
T(4|0) ein Minimum → T(-4|0)
\(f(x)=a*(x-4)^2*(x+4)^2\)
P(0|4)
\(f(0)=a*(0-4)^2*(0+4)^2=256a\)
\(256a=4→a=\frac{1}{64}\)
\(f(x)=\frac{1}{64}*(x-4)^2*(x+4)^2\)