Text erkannt:
Zusammenhang zwischen den Parametern a und c
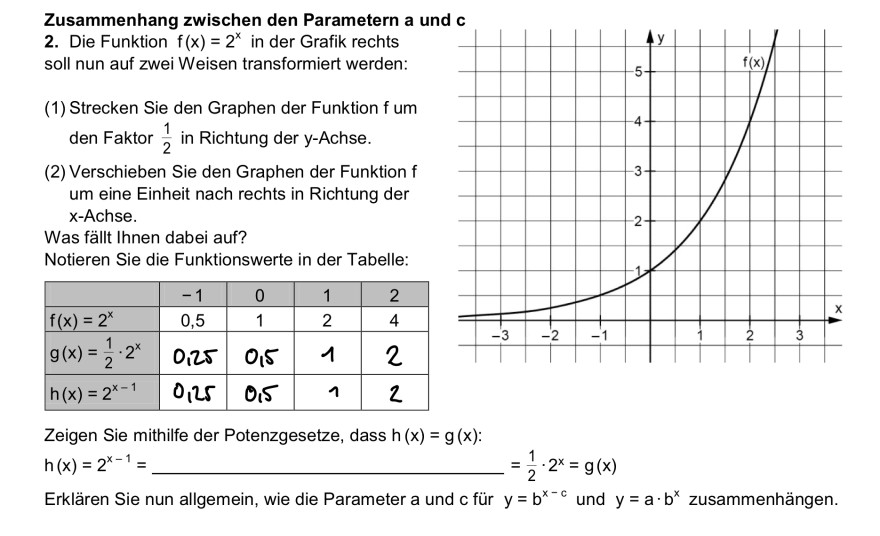
2. Die Funktion \( f(x)=2^{x} \) in der Grafik rechts
soll nun auf zwei Weisen transformiert werden:
(1) Strecken Sie den Graphen der Funktion f um den Faktor \( \frac{1}{2} \) in Richtung der \( \mathrm{y} \)-Achse.
(2) Verschieben Sie den Graphen der Funktion f um eine Einheit nach rechts in Richtung der \( x \)-Achse.
Was fällt Ihnen dabei auf?
Notieren Sie die Funktionswerte in der Tabelle:
\begin{tabular}{|l|c|c|c|c|}
\hline & \( -1 \) & 0 & 1 & 2 \\
\hline\( f(x)=2^{x} \) & 0,5 & 1 & 2 & 4 \\
\hline\( g(x)=\frac{1}{2} \cdot 2^{x} \) & 0,25 & 0,5 & 1 & 2 \\
\hline\( h(x)=2^{x-1} \) & 0,25 & 0,5 & 1 & 2 \\
\hline
\end{tabular}
Zeigen Sie mithilfe der Potenzgesetze, dass \( h(x)=g(x) \) :
\( h(x)=2^{x-1}= \) \( =\frac{1}{2} \cdot 2^{x}=g(x) \)
Erklären Sie nun allgemein, wie die Parameter a und \( c \) für \( y=b^{x-c} \) und \( y=a \cdot b^{x} \) zusammenhängen.