Willkommen in der Mathelounge!
Ein Gerade kann beschrieben werden durch eine Gleichung der (Parameter-)Form:
\(g:\; \vec{x}=\vec{a}+r\cdot \vec{u}\qquad r \in \mathbb{R}\\\)
Dabei heißt A Anbindungspunkt - \( \vec{a} \) Stützvektor der Geraden - und \( \vec{u} \) Richtungsvektor der Geraden.
(Punkt-Richtungs-Form)
Eine Gerade wird auch eindeutig bestimmt durch zwei Punkte A und B (Zwei-Punkte-Form).
\(g:\;\vec{x}=\vec{a}+ r\cdot\overrightarrow{AB}\)
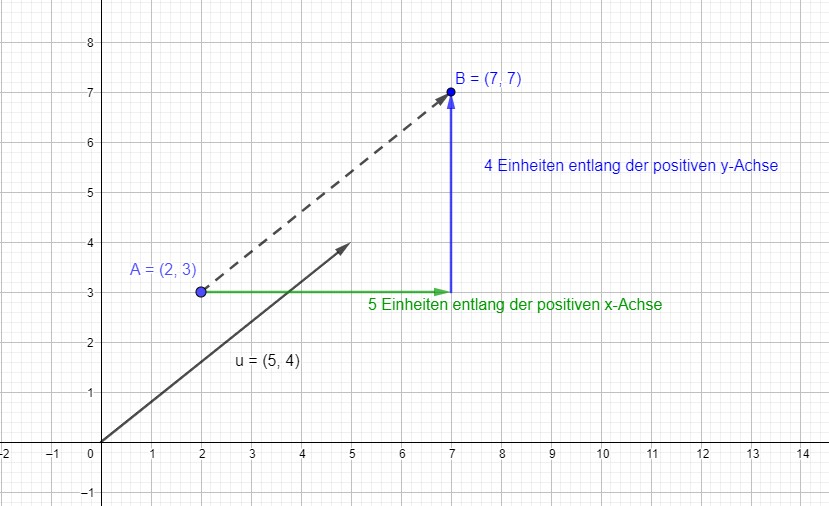
Punkt-Richtungsform: Du hast beispielsweise den Punkt A (2|3) und den Vektor u (5|4)
Dann lautet die Gleichung \(g:\;\vec{x}=\begin{pmatrix} 2\\3 \end{pmatrix}+r\cdot \begin{pmatrix} 5\\4 \end{pmatrix}\)
Für r = 1 ergibt sich der Punkt B(7|7).
Frage nach, wenn noch etwas unklar ist.
Gruß, Silvia