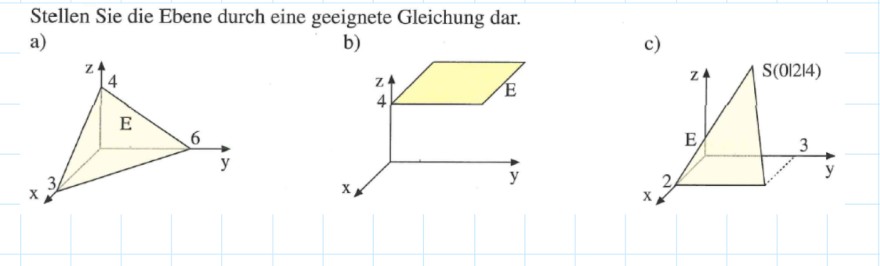
Aufgabe:
Vektorgeometrie: Ebenengleichung anhand eines Bildes erkennen (Normalenform)
Problem/Ansatz:
Es geht nur um Aufgabe b)!
Wie erkenne ich anhand des Bildes, dass der Normalenvektor hier n—> (0/0/1) entspricht? (Lösung)
Meine einzige Erklärung wäre, dass die gesamte Ebene die Höhe 4 hat und ich mit dem Vektor (0/0/1) daher diese Ebene schneide, da diese waagrecht zu mir verläuft.
Wenn das so stimmen sollte, woran erkenne ich, dass die Ebene dieselbe Höhe hat? Dreidimensionale Zeichnungen sind leider bei mir oft Grund zur Verwirrung.
Andernfalls bin ich froh über eine Erklärung, wenn meine Erklärung nicht stimmen sollte.