Funktion berechnen und skizzieren: 2*sin(3*pi*x-1,5*pi)

Question

Ich muss die folgende Funktion skizzieren. Kann mir jemand bitte helfen

 f(x)=2sin(3πx-1,5π)

Answer 1

Hallo !

Die allgemeine Sinusfunktion hat die Form

f(x) = Amplitude * sin(2 * pi / Periodenlänge * (x - X-Verschiebung))

Ich forme also zunächst mal die gegebene Funktion in die allgemeine Form um.

2*sin(3*pi*x-1,5*pi) = 2*sin(2*pi/(2/3)*(x - 0,5))

Die 2 mal vor dem sin ist der Streckfaktor in y-Achsenrichtung. Die Amplidude der normalen Sinusfunktion wachst dadurch von 1 auf 2. Die 3*pi = 2*pi/(2/3) als Faktor vor dem x sind der Stauchfaktor in x-Achsenrichtung, das besagt, dass die Periodenlänge 2/3 ist. Die -1,5 * pi sind für eine Verschiebung auf der x-Achse zuständig. Am besten ist es, wenn man den Faktor vor dem x auch hier ausklammert. Das besagt das unsere Funktion an der x-Koordinate 0,5 wie eine Sinuskurve beginnt.

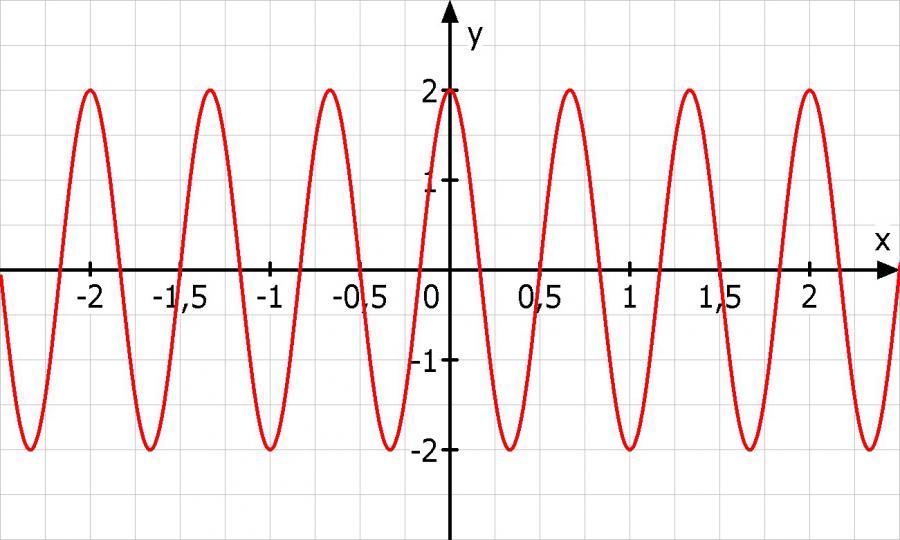
Hier noch eine Zeichnung:

Comments

Danke für die Antwort doch ich verstehe das mit  2*pi/(2/3) nicht so

---

Du hattest

3*pi*x - 1,5*pi

dort Klammer ich jetzt das 3*pi aus

= 3*pi*(x - 0,5*pi)

jetzt schreibe ich den Faktor 3 in dem ich durch (1/3) teile

= pi/(1/3)*(x - 0,5*pi)

am Ende erweitere ich den Bruch noch mit 2 damit oben 2*pi zu stehen kommt

= 2*pi/(2/3)*(x - 0,5*pi)

Hast Du das soweit verstanden?

---

Wieso muss man durch 1/3 teilen?

---

mal 3 ist ja das gleiche wie geteilt durch (1/3) und ich möchte die Periodenlänge ja in den Nenner des Bruches bekommen.

---

Ich zeichne noch mal den Ausschnitt auf den es eigentlich später ankommt.

Hier siehst du den Beginn bei 0,5, die Amplidute von 2 und auch die Periodenlänge von 2/3.

---

ok jetzt hab ich es verstanden. Danke für deine Hilfe.

---

Du kannst aber auch statt einer auch gleich 3 Perioden zeichnen, wegen dem 2/3. Dann haben 3 Perioden hintereinander die Länge 2. Gehen also von 0,5 bis 2,5.

Answer 2

Also. Wie Mathecoach schon geschrieben hat, ist die Amplitude 2:

 

 

Bei diesem Ausschnitt aus dem Graphen, sieht man etwas besser, wo die Kurve die x-Achse schneidet (u.a. bei x=0.5) Es handelt sich bei - 1.5 pi um eine Verschiebung des Graphen um 1.5 pi nach links. Das läuft auf's Gleiche raus, wie eine Verschiebung um 0.5 pi nach rechts. Somit kommt eigentlich ein Cosinus raus: f(x) = 2 cos (3 pi x).

3 pi ist die 'Frequenz'. Die 'normale' Periodenlänge 2 pi ist durch 3 pi zu teilen. Und man bekommt 2/3 als Periode. D.h. bei 0.6666666 ist eine ganze Schwingung fertig.

Rest vgl. andere Antwort