Beispiel: H0: µ0 = 20, H1: µ1 = 25
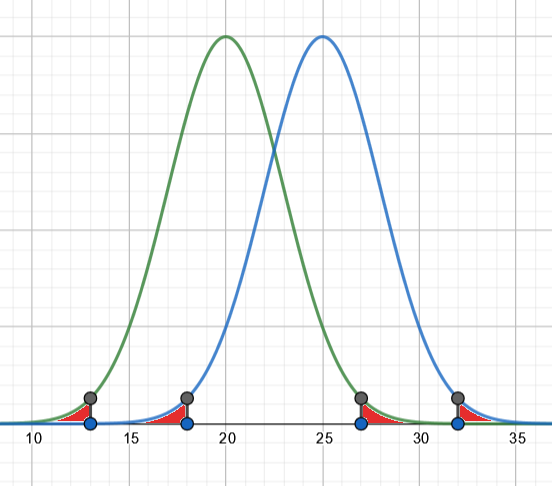
Die rot markierten Bereiche sind die jeweiligen Ablehnungsbereiche. Angenommen das Ergebnis einer Stichprobe liegt im Intervall [20,25], also in keinem der Ablehnungsbereiche, dann kann man daraus weder µ0, noch µ1 als wahr annehmen. Solche Probleme sind nur zu umgehen, wenn die Thesen z.B. H0: µ = x und H1: µ !=x lauten. Abgesehen davon sind bei einem statistischen Test vier Fälle zu unterscheiden:
| X € Annahmebereich
| X € Ablehnungsbereich
|
Hypothese wahr
| Sicherheit 1. Art, p = 1 - α
| Fehler 1. Art, p = α
|
Hypothese falsch
| Fehler 2. Art, p = β
| Sicherheit 2. Art, p = 1 - β
|
Wenn das Ergebnis einer Stichprobe im Annahmebereich liegt, dann gilt eben nicht p(Hypothese wahr) = 1, sondern p(Hypothese wahr) = 1 - α. Während das Niveau α definiert werden kann, kann der Wert β oft nur kompliziert berechnet werden.